Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

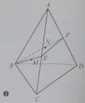
Gọi N, P, Q lần lượt là trung điểm AC, AD, BD thì dễ dàng chứng minh hình thoi MNPQ là thiết diện (việc chứng minh thiết diện là hình thoi cũng vô cùng dễ dàng, 4 cái đường trung bình)
Mặt khác tứ diện đều nên các cặp cạnh đối vuông góc
\(\left\{{}\begin{matrix}AB\perp CD\\AB||MN\\CD||NP\end{matrix}\right.\) \(\Rightarrow MN\perp NP\)
\(\Rightarrow\) Thiết diện là hình vuông cạnh \(\dfrac{a}{2}\)

Trong (ABD), BN cắt AD tại F. Trong (ABC), BM cắt AC tại E.
Do M, N lần lượt là trọng tâm của ∆ABC và ∆ABD nên E, F lần lượt là trung điểm của AC, AD
Tứ diện ABCD có cạnh bằng a nên BE = BF = (a√3)/2
Thiết diện là tam giác cân BEF tại B, có đay EF = a/2
Diện tích BEF là
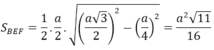
Đáp án D

tham khảo
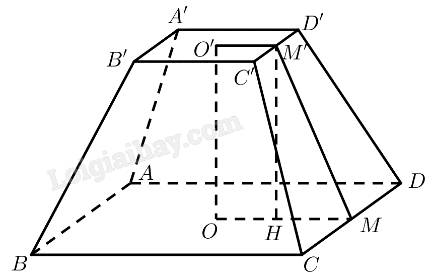
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy.Vậy \(AB=2a,A'B'=a,OO'=2a\)
a)Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'.\)
\(A'B'C'D'\) là hình vuông \(\Rightarrow O'M\perp C'D\)
\(CDD'C\) là hình thang cân \(\Rightarrow MM'\perp C'D'\)
Vậy \(\widehat{MM'O}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ,\(\widehat{M'MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M'H\perp OM\left(H\in OM\right)\)
\(OMM'O'\) là hình chữ nhật
\(\Rightarrow OH=O'M'=\dfrac{a}{2},OM=a,MH=OM-OH=\dfrac{a}{2}\tan\widehat{M'MO}=\dfrac{M'H}{MH}=4\)
\(\Rightarrow\widehat{M'MO}=75,96^o\Rightarrow\widehat{MM'O'}=180^o-\widehat{M'MO}\\ =104,04^o\)
b)Diện tích đáy lớn là:\(S=AB^2=4a^{^2}\)
Diện tích đáy bé là:\(S'=A'B'^2=a^2\)
Thể tích hình chóp cụt là:
\(V_1=\dfrac{1}{3}h\left(S+\sqrt{SS'}+S'\right)\\ =\dfrac{1}{3}.2a\left(4a^2+\sqrt{4a^2.a^2}+a^2\right)=\dfrac{14a^3}{3}\)
Thể tích hình trụ rỗng là:\(V_2=\pi R^2h=\pi\left(\dfrac{a}{2}\right)^2.2a=\dfrac{\pi a^3}{2}\)
Thể tích chân cột là:\(V=V_1-V_2=\left(\dfrac{14}{3}-\dfrac{\pi}{2}\right)a^3\)

Đáp án A
Đặt a> 0 cạnh hình vuông là Dễ thấy
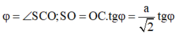
Gọi O là tâm của đáy. Vẽ AH ⊥ SC tại, H, AH cắt SO tại I thì A I O ^ = φ
![]()
Qua I vẽ đường thẳng song song DB cắt SD, SB theo thứ tự tại K, L. Thiết diện chính là tứ giác
ALHK và tứ giác này có hai đường chéo AH ⊥ KL Suy ra
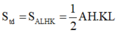
Ta có:


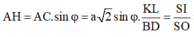
![]()
Theo giả thiết
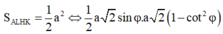
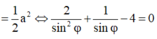
Giải được
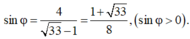
Suy ra φ = a r c sin 33 + 1 8

Đáp án D
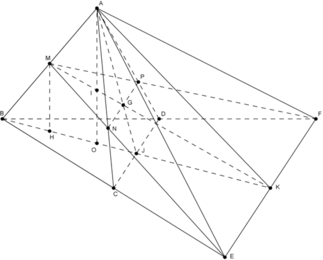
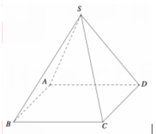
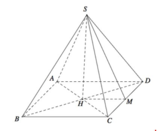
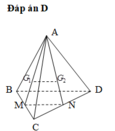
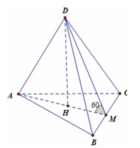
Vẽ AO ⊥ (BCD, MH ⊥ (BCD). Gọi K là trung điểm EF, ta có (ABK) ⊥ (BCD), mp (ABK) chứa AO, MH và là mặt phẳng trung trực của đoạn CD và EF.
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó MG = 1 3 MK (1) và AG = 2 3 AJ hay NP = 2 3 CD = 2 a 3 (vì NP//CD//EF và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là 3 2 a (và diện tích là 3 4 a 2 ).
Tam giác đều BCD cạnh a có đường cao BJ = 3 2 a , trọng tâm O, suy ra BO = 2 3 BJ = a 3 . Lại vì MH là đường trung bình trong tam giác vuông ABO nên
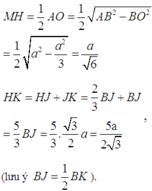
Vì tam giác MHK vuông tại H nên ta có
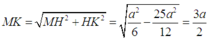
Quay lại (1), ta có
![]()
từ đó tính được diện tích tam giác MNP là
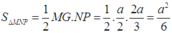
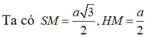
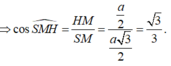
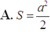


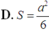

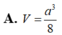
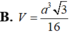
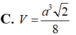
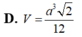

Đáp án B
Gọi O,M lần lượt là trọng tâm tam giác BCD, trung điểm cạnh CD. Khi đó
Do đó