Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
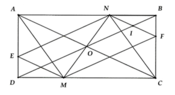
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.

THAM KHẢO
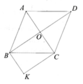
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông

a: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
b: Vì ABCD là hình bình hành
nên AC và BD cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của BD
hay B và D đối xứng nhau qua O
Lời giải:
a)
Vì $ABCD$ là hình thoi nên hai đường chéo $AC$ và $BD$ vuông góc với nhau
\(\Rightarrow \angle DOC=90^0\)
Ta có:
\(\left\{\begin{matrix} DE\parallel AC\\ AC\perp BD\end{matrix}\right.\Rightarrow DE\perp BD\Rightarrow \angle EDB=90^0\)
\(\left\{\begin{matrix} CE\parallel BD\\ BD\perp AC\end{matrix}\right.\Rightarrow CE\perp AC\Rightarrow \angle OCE=90^0\)
Xét tứ giác $ODEC$ có 3 góc đều là góc vuông nên là hình chữ nhật (đpcm)
b) Vì $ODEC$ là hình chữ nhật nên hai đường chéo $CD$ và $OE$ bằng nhau (\(OE=CD)\)
Mà $ABCD$ là hình thoi nên $BC=CD$
\(\Rightarrow OE=BC\) (đpcm)
E cảm ơn cô nhiều ạ