Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đây chỉ là hướng giải, ko phải bài giải nhé ^^!
a) Chứng minh theo dấu hiệu hình hình hành có 1 góc vuông là hcn
b) Cm theo DH Tứ giác có 2 cạnh đối song song và bằng nhau là hình bình hành => AB = OI (2 cạnh đối)
c) Để OBIC là hình vuông thì OB = OC hay BD = AC <=> ABCD là hình vuông

a) tứ giác OBKC có BK // AC (GT) hay BK // OC
CK // BD (gt) hay CK // BO
=> OBKC là HBH ( vì là tứ giác có các cạnh đối //)
^BOC = 90ĐỘ (T/C Hthoi)
=> OBKC là HCN (vì là HBH có 1 góc vuông)
b) OBKC là HCN => OK = BC (t/c HCN) (1)
ABCD là Hthoi (gt) => AB = BC (t/c Hthoi) (2)
từ (1) và (2) => OK = AB
c) Hthoi ABCD cần ĐK ^A = 90ĐỘ để OBKC là Hvuông

THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
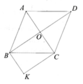

có BI//AC gt / CI//BD BOC=90 độ (tcht) suy ra tứ giác OBIC LÀ hình chữ nhật dkpcm
có OBIC là hình chữ nhật suy ra OI=BC (tchcn) mà BC = AB suy ra OIBAB dkpcm
hình thoi abcd cần có 1 góc vuông hình chữ nhất OIBAB là hình vuông