Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đầu tiên ta chứng minh bổ đề sau:
Cho tam giác \(ABC\) nội tiếp \(\left(O\right)\). Tiếp tuyến tại \(B,C\) của \(\left(O\right)\) cắt nhau tại \(T\). \(TA\) cắt lại \(\left(O\right)\) tại \(D\). \(M\) là trung điểm \(BC\). CM: \(\widehat{BAD}=\widehat{MAC}\).
Giải: Gọi \(L\) là trung điểm \(AD\). Khi đó \(\widehat{OBT}=\widehat{OCT}=\widehat{OLT}=90^o\) nên ngũ giác \(TBLOC\) nội tiếp.
Do vậy, \(\widehat{BLT}=\widehat{BCT}=\widehat{BDC}\). Suy ra cặp góc bù với chúng là \(\widehat{BLD}=\widehat{BAC}\).
Đến đây chứng minh được tam giác \(BLD,BAC\) đồng dạng.
Lập tỉ lệ cạnh rồi dựa vào trung điểm chứng minh được tam giác \(BAD,MAC\) đồng dạng.
Vậy 2 góc cần chứng minh bằng nhau (đpcm).
-------
Trở lại bài toán. (Ở phần dưới mình có dùng tính chất của phương tích và trục đẳng phương. Tuy ko có trong chương trình nhưng nó khá dễ và chứng minh được bằng kiến thức lớp 9. Bạn có thể tự tìm hiểu thêm).
Với lại hình của mình hơi sai một chút, mong bạn thông cảm.
Ý tưởng là ta sẽ chứng minh \(KO\) và hai tiếp tuyến tại \(C,D\) của đường tròn ngoại tiếp tam giác \(DOC\) đồng quy. Nếu làm được điều đó thì theo bổ đề trên sẽ có đpcm.
\(AB\) cắt đường tròn ngoại tiếp tam giác \(AOD,BOC\) lần lượt tại \(E,F\).
Khi đó \(\widehat{EDO}=\widehat{EAO}=\widehat{OCD}\) nên CM được \(ED\) tiếp xúc đường tròn ngoại tiếp tam giác \(DOC\).
CM tương tự thì \(FC\) cũng vậy.
Bây giờ cho \(ED\) cắt \(FC\) tại \(L\).
(Bạn thử tự CM \(LE=LF,LD=LC\) xem).
Do đó \(LE.LD=LF.LC\) nên điểm \(L\) có cùng phương tích đến 2 đường tròn 2 bên.
Vậy điểm \(L\) nằm trên trục đẳng phương của 2 đường tròn này, tức là đường thẳng \(OK\).
Ta đã CM được 3 đường cần CM đồng quy, theo bổ đề suy ra đpcm.

a) Ta thấy: Điểm K nằm trên đường tròn ngoại tiếp \(\Delta\)BDE nên tứ giác DKBE nội tiếp đường tròn
=> ^BEK = ^BDK (2 góc nội tiếp cùng chắn cung BK) hay ^AEK = ^FDK
Mà tứ giác DKFC nội tiếp đường tròn => ^FDK = ^FCK
Nên ^AEK = ^FCK hay ^AEK = ^ACK => Tứ giác AKCE nội tiếp đường tròn
=> ^KAE = ^KCD (Cùng bù ^KCE) hay ^KAB = ^KCD
Do tứ giác BKDE nội tiếp đường tròn nên ^KDE = ^KBA hay ^KBA = ^KDC
Xét \(\Delta\)DKC và \(\Delta\)BKA có: ^KAB = ^KCD; ^KBA = ^KDC => \(\Delta\)DKC ~ \(\Delta\)BKA (g.g)
=> \(\frac{KC}{KA}=\frac{KD}{KB}\Rightarrow\frac{KC}{KD}=\frac{KA}{KB}\).
Đồng thời ^DKC = ^BKA => ^DKC + ^BKC = ^BKA + ^BKC => ^BKD = ^AKC
Xét \(\Delta\)KBD và \(\Delta\)KAC có: ^BKD = ^AKC; \(\frac{KC}{KD}=\frac{KA}{KB}\)=> \(\Delta\)KBD ~ \(\Delta\)KAC (c.g.c)
=> ^KBD = ^KAC hoặc ^KBF = ^KAF => Tứ giác AKFB nội tiếp đường tròn
=> ^BKF = ^BAF (2 góc nội tiếp chắn cung BF) => ^BKF = ^BAC = ^BDC (Do ^BAC và ^BDC cùng chắn cung BC) (1)
Ta có: ^BDC = ^FDC = ^FKC (Cùng chắn cung FC) (2)
Xét \(\Delta\)BMC: ^BMC + ^MBC + ^MCB = 1800. Mà ^MBC = ^BAC; ^MCB = ^BDC (Góc tạo bởi tiếp tuyến và dây cung)
Nên ^BAC + ^BDC + ^BMC = 1800 (3)
Thế (1); (2) vào (3) ta được: ^BKF + ^FKC + ^BMC = 1800 => ^BKC + ^BMC = 1800
=> Tứ giác BKCM nội tiếp đường tròn (đpcm).
b) Ta có: ^BKF = ^BDC (cmt) => ^BKF = ^BDE = ^BKE (Do tứ giác DKBE nội tiếp đường tròn)
Mà 2 điểm F và E nằm cùng phía so với BK => 3 điểm K;F;E thẳng hàng. Hay F nằm trên KE (*)
Mặt khác: ^BKF = ^CKF (Vì ^BKF = ^BAC; ^CKF = ^BDC; ^BAC = ^BDC)
=> ^BKE = ^CKE (Do K;F;E thẳng hàng) => ^KE là phân giác của ^BKC (4)
Xét tứ giác BKCM nội tiếp đường tròn: ^MBC = ^MKC; ^MCB = ^MKB
Lại có: \(\Delta\)BCM cân ở M do MB=MC (T/c 2 tiếp tuyến giao nhau) => ^MBC=^MCB
Từ đó: ^MKC = ^MKB => KM là phân giác của ^BKC (5)
Từ (4) và (5) suy ra: 3 điểm K;M;E thẳng hàng. Hoặc M nằm trên KE (**)
Từ (*) và (**) => 3 điểm E;M;F thẳng hàng (đpcm).

a) CM: \(\widehat{OBM}=\widehat{ODC}\)
\(\widehat{OBM}+\widehat{OBC}=180^o\)( kề bù)
\(\widehat{ODC}+\widehat{OBC}=180^o\)( tứ giác ODCB nội tiếp )
=> \(\widehat{OBM}=\widehat{ODC}\)
b)
+)Xét tam giác MCN có CO là tia phân giác đồng thời là đường cao
=> Tam giác CMN cân tại C (1)
=> \(\widehat{BMA}=\widehat{DNA}=\widehat{BAM}\)( CD//BA => DN//BA)
=> Tam giác BMA cân tại B
=> BM=BA=CD ( ABCD là hình bình hành) (2)
+) CO là phân giác \(\widehat{BCD}\)
=> \(\widebat{BO}=\widebat{DO}\)
=> BO=DO (3)
+) Xét tam giác BOM và tam giác DOC có:
\(\widehat{OBM}=\widehat{ODC}\)( theo a)
BM=CD ( theo 2)
BO=DO (theo 3)
=> \(\Delta BOM=\Delta DOC\)
+) OM=OC
Và từ (1) => CO là đường trung trực của MN
=> OM=ON
Vậy OM=ON=OC
=> O là tâm đường tròn ngoại tiếp tam giác CMN
c) GỌi H là giao của IO và BD
=> IH vuông BD và H là trung điể m BD
Ta có: \(KD^2=\left(HD-HK\right)^2=HD^2+HK^2-2.HD.HK=ID^2-IH^2+IK^2-IH^2-2HD\left(HD-KD\right)\)
\(=ID^2+IK^2-2\left(IH^2+HD^2\right)+2HD.KD=ID^2+IK^2-2ID^2+2HD.KD\)
\(=IK^2-ID^2+2HD.KD\)
=> \(IB^2-IK^2=ID^2-IK^2=2HD.KD-KD^2\)
=> \(\frac{IB^2-IK^2}{KD^2}=\frac{2HD-KD}{KD}=\frac{BD-KD}{KD}=\frac{BK}{KD}\)(4)
Ta lại có: CK là phân giác trong của tam giác CBD
=> \(\frac{BK}{KD}=\frac{CB}{CD}\)
Và MB=DC ( theo cm câu a) , CM=CN ( Tam giác CMN cân)
=> CB=DN
=> \(\frac{BK}{KD}=\frac{DN}{MB}\)(5)
Từ (4), (5)
=> ĐPCM

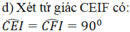
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.