Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(BD\ge AC\Rightarrow BK\ge AH\)
Dễ dàng CM: \(BK+AH\ge AB+CD\)(1)
Mà \(2BK\ge BK+AH\left(2\right)\)
Từ (1) và (2) suy ra :
\(BK\ge\frac{AB+CD}{2}=\frac{S_{ABCD}}{DK}=\frac{1}{DK}\)
Vậy ta có: \(BD^2=BK^2+DK^2\ge DK^2+\frac{1}{DK^2}\ge2\Rightarrow BD\ge\sqrt{2}\)

a: Xét tứ giác ABDE có
AB//DE
AE//BD
=>ABDE là hbh
=>AB=DE=5cm và BD=AE=12cm
EC=5+15=20cm
EC^2=AE^2+AC^2
=>ΔAEC vuông tại A
b: Kẻ AH vuông góc EC tại H
=>AH=15*20/25=300/25=12cm
S ABCD=1/2*AH*(AB+CD)
=1/2*12*(5+15)=20*6=120cm2

Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC
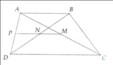

Kẻ AN cắt CD tại E
Xét △ANB và △END có :
^ANB = ^END (đối đỉnh)
NB = ND (gt)
^ABD = ^BDE (so le trong)
\(\Rightarrow\)△ANB = △END (g.c.g)
\(\Rightarrow\)AN = NE (cặp cạnh tương ứng)
Xét △AEC có : AM = MC
AN = NE
\(\Rightarrow\)MN // EC
\(\Rightarrow\)MN // AB // CD (ĐPCM)