Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC
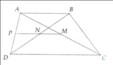

a, gọi MN cắt BC tại O
xét tam giácBDC có : M là trung điểm của BD (gt)
MO // DC (Gt)
=> O là trung điểm của BC (đl)
xét tam giác ABC có : NO // AB
=> N là trung điểm của AB (đl)

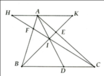
Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC

Trong ΔADB, ta có: MN // AB (gt)
Suy ra: ![]() hệ quả định lí ta-lét) (1)
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: 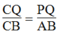 Hệ quá định lí Ta-lét) (2)
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: ![]() (Định lí Ta-lét) (3)
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra ![]() hay MN = PQ.
hay MN = PQ.

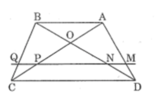
Kẻ AN cắt CD tại E
Xét △ANB và △END có :
^ANB = ^END (đối đỉnh)
NB = ND (gt)
^ABD = ^BDE (so le trong)
\(\Rightarrow\)△ANB = △END (g.c.g)
\(\Rightarrow\)AN = NE (cặp cạnh tương ứng)
Xét △AEC có : AM = MC
AN = NE
\(\Rightarrow\)MN // EC
\(\Rightarrow\)MN // AB // CD (ĐPCM)