Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
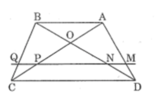
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: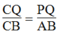 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra 
hay MN = PQ.
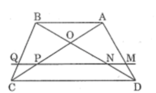
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: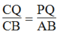 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: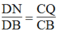 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra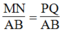 
hay MN = PQ.
a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ
Xét Tam giác ADB: MN // AB (gt)
Suy ra: DN/DB = MN/AB (Hệ quả định lí Talét) (1)
Xét Tam giác ACB: PQ // AB (gt)
Suy ra: CQ/CB = PQ/AB (Hệ quá định lí Talét) (2)
Ta có: NQ sog sog AB (gt)
AB sog sog CD (gt)
Suy ra: NQ sog sog CD (cùng sog sog AB)
Xét Tam giác BDC: NQ sog sog CD (cmt)
Suy ra: DN/DB = CQ/CB (Định lí Talét) (3)
Từ (1), (2) và (3) suy ra: MN/AB = PQ/AB
Suy ra: MN = PQ (đpcm).
Để chứng minh rằng MN=PQ, ta sẽ sử dụng tính chất của các tam giác đồng dạng.
Gọi X là giao điểm của MQ và NP.
Ta có các tam giác đồng dạng sau:
MQX và NPX (do MQ song song với NP, XM song song với PN và góc MXQ và PXN là góc đồng phía nội tiếp giữa hai đoạn thẳng MQ và NP).XMD và XCB (do MQ song song với CB và MD song song với BX).XNC và XAD (do NP song song với AD và NC song song với XA).
Từ tính chất của các tam giác đồng dạng, ta có thể viết các tỉ số tương ứng:
(1)PNMQ=PXQX(1)(2)CBMD=XBXM(2)(3)ADNC=AXNX(3)
Như vậy, từ các phương trình trên, ta có thể suy ra:
(4)PNMQ=CBMD⋅ADNC(4)
Vậy nên ta thấy rằng PNMQ=CBMD⋅ADNC.
Từ (4), ta thấy rằng MQ=PN khi và chỉ khi MD=NC, CB=AD, tức là ABCD là hình vuông.
Do đó, ta đã chứng minh được rằng MN=PQ khi và chỉ khi ABCD là hình vuông.
mong là đúng:))
Đường thẳng song song với \(AB\) cắt và \(BC\) theo thứ tự tại các điểm \(M,N,P,Q\) nên
\(PM//AB//CD;MN//AB//CD;NQ//AB//CD\).
- Xét tam giác \(BCD\) có \(QN//CD\) và \(QN\) cắt \(BD;BC\) lần lượt tại \(N;Q\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{QN}}{{DC}} = \frac{{NB}}{{BD}} = \frac{{BQ}}{{BC}} \Rightarrow \frac{{QN}}{{DC}} = \frac{{NB}}{{BD}}\) (1)
- Xét tam giác \(ACD\) có \(PM//CD\) và \(PM\) cắt \(AD;AC\) lần lượt tại \(M;P\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{PM}}{{DC}} = \frac{{PA}}{{AC}} = \frac{{AM}}{{AD}} \Rightarrow \frac{{PM}}{{DC}} = \frac{{AM}}{{AD}}\) (2)
- Xét tam giác \(DMN\) có \(AB//MN\). Theo định lí Thales ta có:
\(\frac{{AM}}{{AD}} = \frac{{NB}}{{BD}}\) (3)
Từ (1), (2), (3) ta có:
\(\frac{{AM}}{{AD}} = \frac{{NB}}{{BD}} = \frac{{QN}}{{DC}} = \frac{{PM}}{{DC}} \Rightarrow \frac{{QN}}{{DC}} = \frac{{PM}}{{DC}} \Rightarrow QN = PM\)
Ta có:
\(QN + MQ = PM + MQ \Rightarrow MN = PQ\) (đpcm).
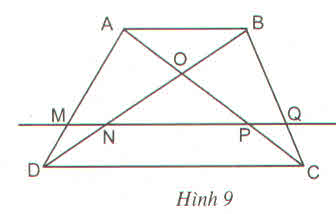
Trong tam giác ADBADB, ta có: MNMN // ABAB (gt)
Suy ra DNDB =MNABDBDN =ABMN (hệ quả định lí Thalès) (1)
Trong tam giác ACBACB, ta có: PQPQ // ABAB (gt)
Suy ra CQCB =PQABCBCQ =ABPQ (hệ quả định lí Thalès) (2)
Lại có: NQNQ // ABAB (gt); ABAB // CDCD (gt)
Suy ra NQNQ // CDCD
Trong tam giác BDCBDC, ta có: NQNQ // CDCD (chứng minh trên)
Suy ra DNDB =CQCBDBDN =CBCQ (định lí Thalès) (3)
Từ (1), (2) và (3) suy ra MNAB =PQAB hayABMN =ABPQ hayMN = PQ$ (đpcm).