Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
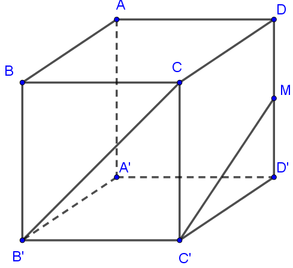
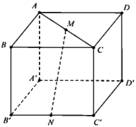
Gọi E là trung điểm A’B’. Khi đó ANC’E là hình bình hành. Suy ra C’N song song với AE. Như vậy góc giữa hai đường thẳng BM và C’N bằng góc giữa hai đường thẳng BM và AE. Ta có Δ M A B = Δ E A ’ A c − g − c suy ra A ' A E ^ = A B M ^ (hai góc tương ứng).
Do đó: A ' A E ^ + B M A ^ = A B M ^ + B M A ^ = 90 0 . Suy ra hai đường thẳng BM và AE vuông góc với nhau nên góc gữa chúng bằng 90 0 . Vậy góc giữa hai đường thẳng BM và C’N bằng 90 0 .
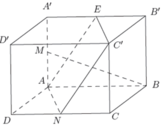

Gọi cạnh của hình lập phương là a.
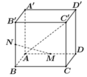
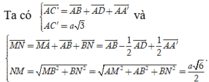
Suy ra
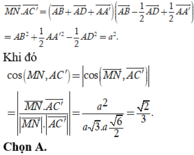
Cách 2. Gọi độ dài cạnh hình lập phương A B C D . A ' B ' C ' D ' là
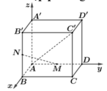
Chọn hệ trục tọa độ Oxyz sao cho ![]()
Khi đó, tọa độ các đỉnh:

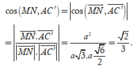

Đáp án A
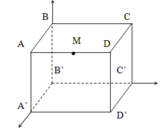
Giả sử AB = x
B ' ( 0 ; 0 ; 0 ) , A ' ( x ; 0 ; 0 ) , C ' ( 0 ; 4 a ; 0 ) , M ( x ; 2 a ; 2 a ) A ' B ' → ( x ; 0 ; 0 ) , C ' M → ( x ; − 2 a ; 2 a ) , B ' C ' → ( 0 ; 4 a ; 0 ) [ A ' B ' → , C ' M → ] = ( 0 ; − 2 a x ; − 2 a x ) d ( A ' B ' ; C ' M ) = [ A ' B ' → , C ' M → ] B ' C ' → [ A ' B ' → , C ' M → ] = − 8 a 2 x 8 a 2 x 2 = 2 2 a

Đáp án D.
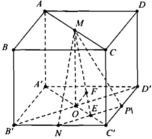
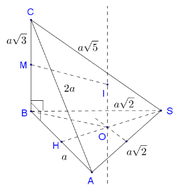
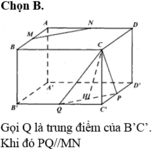
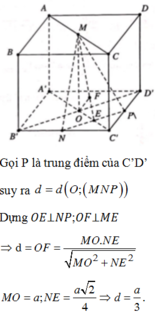
Gọi P là trung điểm của C’D’ suy ra d = d O ; M N P
Dựng:
O A ⊥ N P ; OF ⊥ ME ⇒ d=OF= M O . N E M O 2 + N E 2
trong đó
M O = a ; N E = a 2 4 ⇒ d = a 3 .

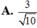

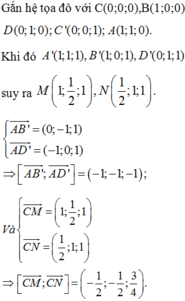
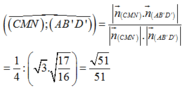

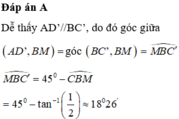
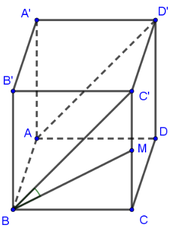
Đáp án D
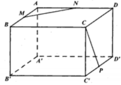
Giả sử hình lập phương có cạnh là 1.
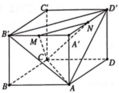
A ' C // A C ⇒ A C , C ' M ^ = A ' C ' , C ' M ^
Xét Δ A ' C ' M ' có:
A ' C ' = 2 , C ' M = 1 2 + 1 2 2 = 5 2 , A ' M = A ' D 2 + M D 2 = 2 + 1 4 = 3 2
Định lí Cô sin: a 2 = b 2 + c 2 − 2 b c cos A ⇒ cos A = b 2 + c 2 − a 2 2 b c ta được: cos A C , C ' M ^ = 1 10 .