K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2022
Do \(\left\{{}\begin{matrix}AA'\perp\left(ABCD\right)\Rightarrow AA'\perp AD\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(AA'C\right)\)
Mà \(AD||A'D'\Rightarrow A'D'\perp\left(AA'C\right)\)
Lại có \(AA'||CC'\Rightarrow C'\in\left(AA'C\right)\Rightarrow A'D'\perp AC'\) (1)
\(\left\{{}\begin{matrix}AA'\perp AC\\AA'=AC\end{matrix}\right.\) \(\Rightarrow\) tứ giác AA'C'C là hình vuông
\(\Rightarrow AC'\perp A'C\) (2)
(1);(2) \(\Rightarrow AC'\perp\left(A'D'C\right)\)
NT
0

1N
0

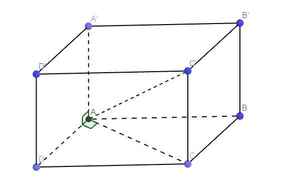
a) AC // A’C’, D’C // A’B \( \Rightarrow \) (D'AC) // (BC'A')
Ta có \(AC \bot BD,AC \bot BB' \Rightarrow AC \bot \left( {BDB'} \right);B'D \subset \left( {BDB'} \right) \Rightarrow AC \bot B'D\)
Mà AC // A’C’ \( \Rightarrow \) \(B'D \bot A'C'\)
Ta có \(AB' \bot A'B,AD \bot A'B \Rightarrow A'B \bot \left( {AB'D} \right);B'D \subset \left( {AB'D} \right) \Rightarrow A'B \bot B'D\)
Mà A’B // D’C \( \Rightarrow \) \(B'D \bot D'C\)
Ta có \(B'D \bot AC,B'D \bot D'C \Rightarrow B'D \bot \left( {D'AC} \right)\)
\(B'D \bot A'C',B'D \bot A'B \Rightarrow B'D \bot \left( {BA'C'} \right)\)
b) Gọi \(AC \cap BD = \left\{ O \right\},A'C' \cap B'D' = \left\{ {O'} \right\}\)
Trong (BB’D’D) nối \(D'O \cap B'D = \left\{ E \right\},BO' \cap B'D = \left\{ F \right\}\)
Vì (D'AC) // (BC'A') nên d((D'AC), (BC'A')) = d(E, (BC'A')) = EF do \(B'D \bot \left( {BA'C'} \right)\)
\(\left. \begin{array}{l}B'D \bot BO'\left( {B'D \bot \left( {BA'C'} \right)} \right)\\B'D \bot OD'\left( {B'D \bot \left( {D'AC} \right)} \right)\end{array} \right\} \Rightarrow BO'//OD'\)
Áp dụng định lí Talet có \(\frac{{DE}}{{EF}} = \frac{{DO}}{{BO}} = 1 \Rightarrow DE = EF\) và \(\frac{{B'F}}{{EF}} = \frac{{B'O'}}{{O'D'}} = 1 \Rightarrow B'F = EF\)
\( \Rightarrow EF = \frac{{B'D}}{3}\)
Xét tam giác ABD vuông tại A có \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Xét tam giác BB’D vuông tại B có \(B'D = \sqrt {B{{B'}^2} + B{D^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 3 \)
\( \Rightarrow EF = \frac{{a\sqrt 3 }}{3}\)
Vậy \(d\left( {\left( {D'AC} \right),{\rm{ }}\left( {BC'A'} \right)} \right) = \frac{{a\sqrt 3 }}{3}\)