Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

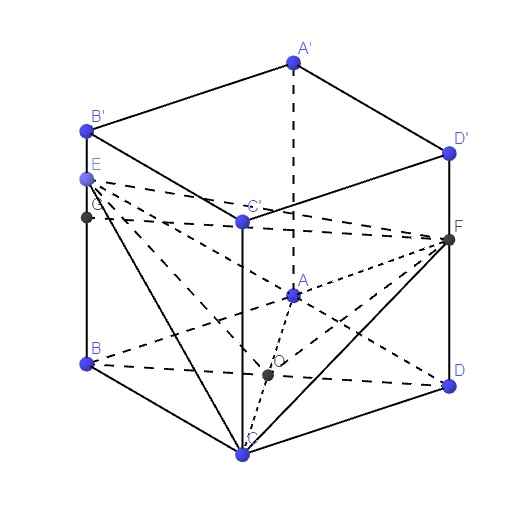
Gọi O là giao điểm AC và BD
Do lăng trụ đều \(\Rightarrow AC\perp\left(BDD'B'\right)\Rightarrow AC\perp\left(EOF\right)\)
\(V_{ACEF}=V_{AOEF}+V_{COEF}=2V_{AOEF}=\dfrac{2}{3}AO.S_{OEF}=\dfrac{a\sqrt{2}}{3}.S_{OEF}\)
Đặt \(BE=x;\) \(DF=y\), trên BB' lấy G sao cho \(BG=DF=y\)
\(\Rightarrow FG=BD=a\sqrt{2}\) và \(EG=\left|x-y\right|\)
\(\Rightarrow EF=\sqrt{EG^2+FG^2}=\sqrt{2a^2+\left(x-y\right)^2}\)
\(OE=\sqrt{OB^2+BE^2}=\sqrt{\dfrac{a^2}{2}+x^2}\) ; \(OF=\sqrt{OD^2+DF^2}=\sqrt{\dfrac{a^2}{2}+y^2}\)
Do \(\left(EAC\right)\perp\left(FAC\right)\Rightarrow OE\perp OF\)
\(\Rightarrow OE^2+OF^2=EF^2\)
\(\Rightarrow a^2+x^2+y^2=2a^2+\left(x-y\right)^2\Rightarrow xy=\dfrac{a^2}{2}\)
\(S_{OEF}=\dfrac{1}{2}OE.OF=\dfrac{1}{2}\sqrt{\left(\dfrac{a^2}{2}+x^2\right)\left(\dfrac{a^2}{2}+y^2\right)}=\dfrac{1}{2}\sqrt{\dfrac{a^4}{4}+\left(xy\right)^2+\dfrac{a^2}{2}\left(x^2+y^2\right)}\)
\(=\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+\dfrac{a^2}{2}\left(x^2+y^2\right)}\ge\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+\dfrac{a^2}{2}.2xy}=\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+a^2.\dfrac{a^2}{2}}=\dfrac{a^2}{2}\)
\(\Rightarrow V_{ACEF}\ge\dfrac{a\sqrt{2}}{3}.\dfrac{a^2}{2}=\dfrac{a^3\sqrt{2}}{6}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{a\sqrt{2}}{2}\)

Đáp số: \(\dfrac{a\sqrt{2}}{4}\) .
Dễ thấy đường thẳng IJ song song với mặt phẳng (BB'D'D) nên khoảng cách giữa 2 đường thẳng IJ và B'D' bằng khoảng cách giữa đường thẳng IJ và mặt phẳng (BB'D'D) bằng khoảng cách từ điểm J tới mặt phẳng (BB'D'D).
Mặt khác, A'C' vuông góc với B'D' và Đ' nên A'C' vuông góc với (BB'D'D). Gọi O' là giao điểm 2 đường chéo B'D' và A'C'; E là trung điểm đoạn B'O thì JE là đường trung bình tam giác B'OC' nên \(JE\)vuông góc với (BB'D'D) và bằng \(\dfrac{1}{2}OC'=\dfrac{1}{4}A'C'=\dfrac{a\sqrt{2}}{4}\).

\(B'N=2BN\Rightarrow BN=\dfrac{1}{3}BB'=2a\)
Qua N lần lượt kẻ các đường thẳng song song AB và BC, chúng cắt AA' tại E và CC' tại F
\(\Rightarrow AE=BN=CF=2a\Rightarrow PF=ME=\dfrac{6a}{2}-2a=a\)
\(NF=NE=AB=BC=a\)
\(\Rightarrow MN=NP=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow S_{MNP}=\dfrac{a^2\sqrt{7}}{4}\) (công thức Herong, hoặc kẻ NH vuông góc MP và tính NH theo Pitago với tam giác MNP cân tại N)
\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
Do MA, NB, PC vuông góc (ABC) \(\Rightarrow\) ABC là hình chiếu vuông góc của MNP lên (ABC)
\(\Rightarrow cos\alpha=\dfrac{S_{ABC}}{S_{MNP}}=\sqrt{\dfrac{3}{7}}\Rightarrow\alpha\)

Trong mặt phẳng (ABCD), kéo dài AM cắt DC tại E \(\Rightarrow\) C là trung điểm DE (t/c đường trung bình)
Trong mặt phẳng CDD'C' nối EI kéo dài lần lượt cắt CC' và DD' tại P và Q
Mặt phẳng (AMI) cắt lập phương theo thiết diện là tứ giác AMPQ
Gọi N là trung điểm CD \(\Rightarrow\left\{{}\begin{matrix}IN//DD'\\CN=\frac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\frac{EN}{ED}=\frac{\frac{3a}{2}}{2a}=\frac{3}{4}\)
Talet: \(\frac{EN}{ED}=\frac{IN}{DQ}=\frac{3}{4}\Rightarrow DQ=\frac{4}{3}IN=\frac{4}{3}.\frac{a}{2}=\frac{2a}{3}\)
\(CP=\frac{1}{2}DQ=\frac{a}{3}\) (đường trung bình)
\(V_{MCP.ADQ}=V_{E.ADQ}-V_{E.MCP}=\frac{1}{6}\left(ED.AD.DQ-EC.MC.CP\right)\)
\(=\frac{1}{6}\left(2a.a.\frac{2a}{3}-a.\frac{a}{2}.\frac{a}{3}\right)=\frac{7a^3}{36}\)
\(\Rightarrow V=V_{ABCD.A'B'C'D'}-\frac{7a^3}{26}=a^3-\frac{7a^3}{36}=\frac{29a^3}{36}\)
Bạn thử tải app này xem có đáp án không nhé <3 https://giaingay.com.vn/downapp.html