Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
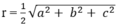
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )

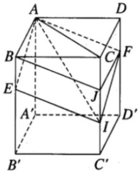
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.
Từ đó suy ra IJ = EB = DF = JC = c/3
Ta có
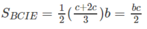
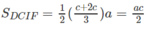
Nên V H = V A . BCIE + V A . DCIF
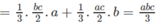
Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên
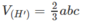
Từ đó suy ra 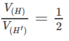

Đáp án B
Xét lăng trụ (T) có:
![]()
Xét mặt cầu (C) có: R C = A P 2 = a 3
![]()
Tỉ số bằng 8 4 3 = 2 3 3

Đáp án A
A B C D . A ' B ' C ' D ' nội tiếp khối lăng trụ, ABCD.MNPQ nội tiếp mặt cầu nên
A B C D . A ' B ' C ' D ' là hình hộp chữ nhật
Bán kính đường tròn ngoại tiếp
ABCD là r = 2 a , V T = 4 a . π . 2 a 2 = 8 πa 3
Bán kính mặt cầu ngoại tiếp ABCD.MNPQ là
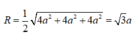
![]()
Vậy V ( T ) V ( C ) = 8 πa 3 4 3 πa 3 = 2 3 3

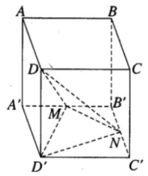
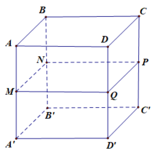
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
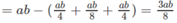
Thể tích khối chóp
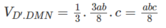
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8

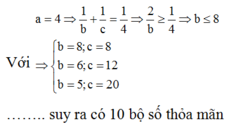
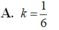
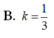
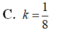
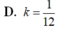
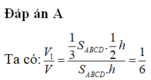


Chọn B.
Giả sử khối hộp chữ nhật có ba kích thước là a, b, c.
Khi đó thể tích khối hộp chữ nhật là: V = abc.
Từ giả thiết ta có
Vậy thể tích V của khối hình hộp chữ nhật gần nhất với giá trị 592.