Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
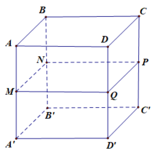
A B C D . A ' B ' C ' D ' nội tiếp khối lăng trụ, ABCD.MNPQ nội tiếp mặt cầu nên
A B C D . A ' B ' C ' D ' là hình hộp chữ nhật
Bán kính đường tròn ngoại tiếp
ABCD là r = 2 a , V T = 4 a . π . 2 a 2 = 8 πa 3
Bán kính mặt cầu ngoại tiếp ABCD.MNPQ là
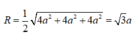
![]()
Vậy V ( T ) V ( C ) = 8 πa 3 4 3 πa 3 = 2 3 3

Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)

5.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\)
\(\Rightarrow BC\perp\left(A'AM\right)\)
\(\Rightarrow\widehat{A'MA}\) là góc giữa (A'BC) và (ABC)
\(\Rightarrow\widehat{A'MA}=60^0\)
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow A'A=AM.tan60^0=\frac{3a}{2}\)
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=B.A'A=\frac{3\sqrt{3}}{8}a^3\)
1.
\(V=Bh\)
2.
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=Bh=\frac{a^2\sqrt{3}}{4}.a\sqrt{6}=\frac{3\sqrt{2}}{4}a^3\)
3.
\(B=\frac{1}{2}\left(a\sqrt{2}\right)^2=a^2\Rightarrow V=Bh=a^2.5a=5a^3\)
4.
\(h=\sqrt{\left(2a\right)^2-\left(a\sqrt{3}\right)^2}=a\)
\(B=\frac{\left(a\sqrt{3}\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}a^2\)
\(V=Bh=\frac{3\sqrt{3}}{4}a^3\)

4.
Qua G kẻ đường thẳng song song AB lần lượt cắt AC và BC tại M và N
\(\Rightarrow A'B'NM\) là thiết diện của (A'B'G) và lăng trụ
Theo Talet ta có \(\frac{CM}{AC}=\frac{CN}{BC}=\frac{2}{3}\Rightarrow CM=CN=\frac{2a}{3}\)
Kéo dài A'M, B'N, C'C đồng quy tại P (theo tính chất giao tuyến 3 mặt phẳng)
Do \(CN//B'C'\Rightarrow\frac{PC}{PC'}=\frac{CN}{B'C'}=\frac{2}{3}\Rightarrow\frac{PC}{PC+CC'}=\frac{2}{3}\)
\(\Rightarrow3PC=2\left(PC+a\right)\Rightarrow PC=2a\)
\(\Rightarrow PC'=3a\)
\(MN=\frac{2}{3}BC\Rightarrow S_{CMN}=\frac{4}{9}S_{ABC}=\frac{4}{9}.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{9}\)
\(V_{P.A'B'C'}=\frac{1}{3}PC'.S_{A'B'C'}=\frac{1}{3}.3a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{4}\)
\(V_{P.CMN}=\frac{1}{3}PC.S_{CMN}=\frac{1}{3}.2a.\frac{a^2\sqrt{3}}{9}=\frac{2a^3\sqrt{3}}{27}\)
\(\Rightarrow V_{CMN.A'B'C'}=\frac{a^3\sqrt{3}}{4}-\frac{2a^3\sqrt{3}}{27}=\frac{19a^3\sqrt{3}}{108}\)
\(\Rightarrow V_{MNABA'B'}=\frac{a^3\sqrt{3}}{4}-\frac{19a^3\sqrt{3}}{108}=\frac{2a^3\sqrt{3}}{27}\)
2.
Đề thiếu dữ kiện ko tính được, chỉ tính được trong trường hợp tam giác ABC là vuông cân.
3.
\(AC=BC=a\sqrt{2}\) ; \(AC=AB\sqrt{2}=2a\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{BA'M}\) là góc giữa A'B và (ACC'A')
\(\Rightarrow\widehat{BA'M}=30^0\)
\(BM=\frac{1}{2}AC=a\)
\(tan\widehat{BA'M}=\frac{BM}{A'M}\Rightarrow A'M=\frac{BM}{tan30^0}=a\sqrt{3}\)
\(A'A=\sqrt{A'M^2-AM^2}=a\sqrt{2}\)
\(V=\frac{1}{2}A'A.AB.BC=a^3\sqrt{2}\)
Ko đáp án nào đúng
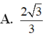
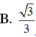
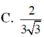
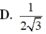
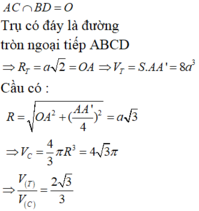
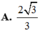
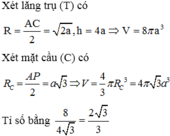
 A.3a3 B.a3 C.a3
A.3a3 B.a3 C.a3
Đáp án B
Xét lăng trụ (T) có:
Xét mặt cầu (C) có: R C = A P 2 = a 3
Tỉ số bằng 8 4 3 = 2 3 3