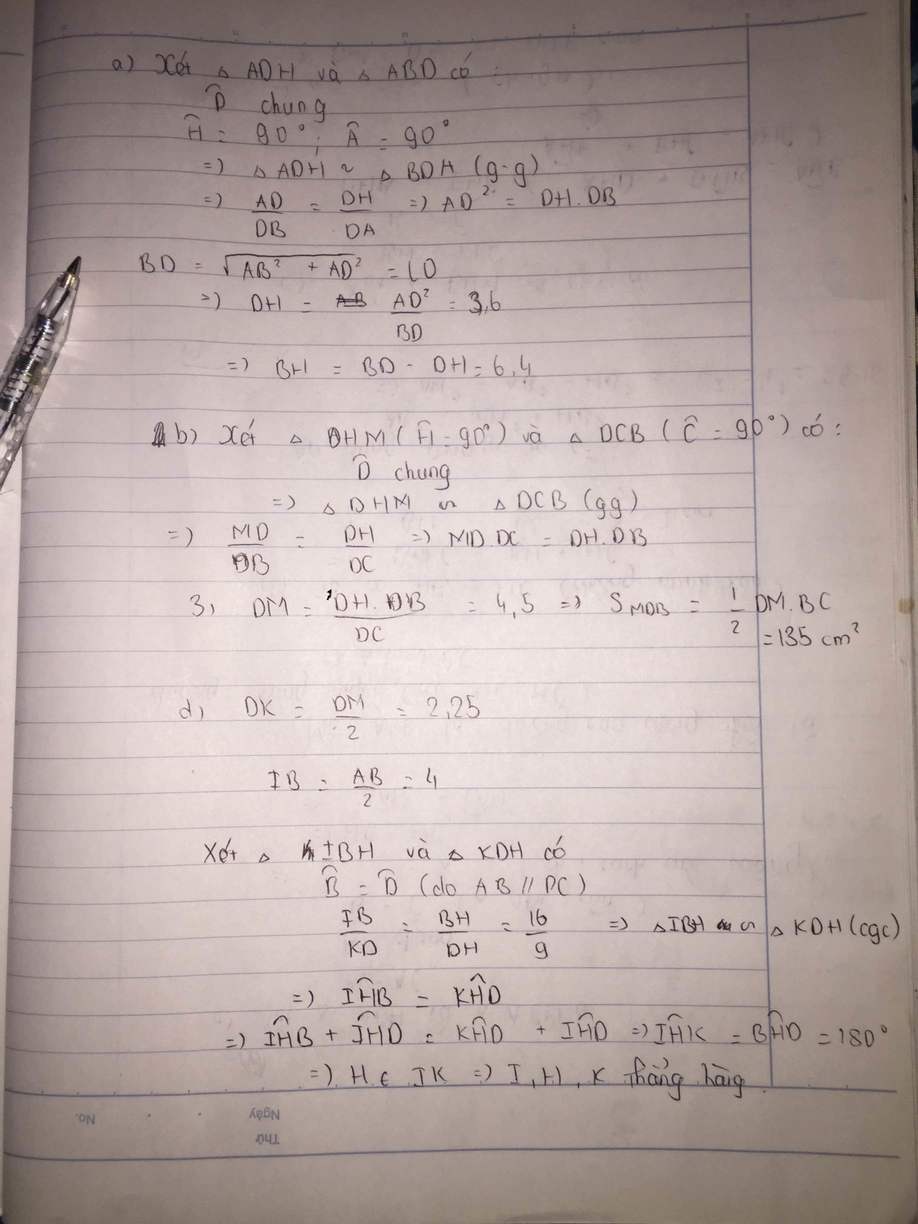Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bn tự kẻ hình nha!!
Gọi I là trung điểm của AH
Ta có IM là đg trug bình t.giác AHB
- -> IM=1/2AB và IM sog sog vs AB
- ->IMND là hình bình hành
- ->DI sog sog vs MN(1)
Do IM sog sog vs AB->IM vuông góc vs AD
Tg ADM có các đg cao AH và MI cắt nhau tại I
- -> DI vuông góc vs AM(2)
Từ (1) và (2) suy ra AM vuông góc vs MN
Tg AMN vuông tại M
Ta có :AM^2+MN^2=AN^2
Lại có:Tg ADN vuông tại D
- ->AN^2=AD^2+DN^2+AD^2/4=4^2+3^2=25
- Vậy MA^2+NM^2=25
vì sao IMND là hình bình hành vậy.
Nếu bài này ko cm như trên mà chứng minh MA vuông góc MN thì làm như nào ạ .

a: BD=căn 8^2+6^2=10cm
AH=6*8/10=4,8cm
b: Xét ΔADH vuông tại H và ΔCBA vuông tại A có
góc ADH=góc BCA
=>ΔADH đồng dạng với ΔCBA
c: Xét ΔADM và ΔACN có
AD/AC=DM/CN
góc ADM=góc ACN
=>ΔADM đồng dạng với ΔACN

a: \(AC=\sqrt{15^2+8^2}=17\left(cm\right)\)
OD=AC/2=8,5cm
b: Xét tứ giác ADPC có
M là trung điểm chung của AP và DC
nên ADPC là hình bình hành
=>DP=AC=2OC
c: Xét tứ giác OBEC có
N là trung điểm chung của OE và bC
OB=OC
Do dó: OBEC là hình thoi

a) Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
\(\widehat{ABD}\) chung
Do đó: ΔAHD∼ΔBAD(g-g)
Áp dụng định lí Pytago vào ΔADH vuông tại H, ta được:
\(AH^2+HD^2=AD^2\)
\(\Leftrightarrow HD^2=AD^2-AH^2=5^2-4^2=9\)
hay HD=3(cm)
Ta có: ΔAHD∼ΔBAD(cmt)
nên \(\dfrac{AH}{BA}=\dfrac{HD}{AD}=\dfrac{AD}{BD}\)
\(\Leftrightarrow\dfrac{4}{AB}=\dfrac{3}{5}\)
hay \(AB=\dfrac{20}{5}cm\)
Vậy: \(AB=\dfrac{20}{5}cm\)
b) Xét ΔAHD vuông tại H và ΔBHA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\left(=90^0-\widehat{ADH}\right)\)
Do đó: ΔAHD∼ΔBHA(g-g)
⇔\(\dfrac{AH}{BH}=\dfrac{HD}{HA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(HA^2=HB\cdot HD\)(đpcm)