Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔAHD vuông tại H và ΔDCB vuông tại C có
góc ADH=góc DBC
=>ΔAHD đồng dạng vơi ΔDCB
c: Xét ΔHAB có HN/HA=HM/HB
nên MN//AB
=>MN vuông góc AD
mà AH vuông góc DM
và AH cắt MN tại N
nên N là trực tâm
=>ND vuông góc AM
=>ME vuông góc AM

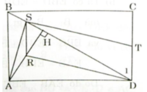
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
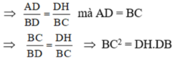
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
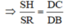
![]()
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o

a: Xét ΔHAB có
N là trung điểm của HB
M là trung điểm của HA
Do đó: NM là đường trung bình của ΔAHB
Suy ra: \(NM=\dfrac{AB}{2}=2\left(cm\right)\)

a: Xét ΔHAD có HM/HA=HN/HD
nên MN//AD
b: Xét ΔHAD có MN//AD
nên MN/AD=HM/HA=1/2
=>MN=1/2AD=1/2BC
=>MN=BI
mà MN//BI
nên BMNI là hình bình hành
a, xét tam giác ADH và tam giác DBC có:
góc AHD=góc BCD=90 độ
góc ADH= góc DBC (so le trong)
=> tam giác ADH~tam giác DBC
=> AD/DB=DH/BC
mà AD=BC (ABCD là hcn)
=> BC/DB=DH/BC
=> BC.BC=DH.DB
hay \(BC^2\)= DH.DB
b, xét tam giác HAB có:
AN=HN (N là trung điểm của AH)
HM=BM (M là trung đểm của HB)
=> MN là đg tb của tam giác HAB
=> MN//AB
=> tam giác HMN~ tam giác HBA
c, xét tam giác HBA và tam giác CDB có:
góc AHB=góc BCD=90 độ
góc ABH=góc BDC (so le trong)
=> tam giác HBA~tam giác CDB
mà tam giác HBA~tam giác HMN (theo b)
=> tam giác HMN~tam giác CDB
=> HM/CD=MN/BD
=> HM.BD=MN.CD
mình biết làm 3 phần thôi ạ