Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
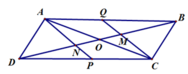
Vì nếu M là tâm đường tròn ngoại tiếp tam giác suy ra MA = MC nên tam giác MAC cân tại M suy ra MO vuông góc AC suy ra ABCD là hình thoi (vô lý)

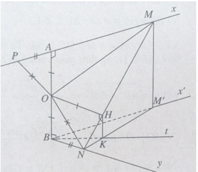
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
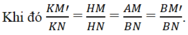
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

Có MC=2MI mà MI là đường trung tuyến của của \(\Delta ABC\)
=>M là trọng tâm của tam giác ABC=>A,M,H thẳng hàngTrong mp(SAH)có :AN=2NS;AM=2MH=>MN//SH (Thales)Mà \(SH\perp\left(ABC\right)\);SH ko thuộc (ABC)=>MN vuông góc với (ABC)
P/s: Gợi ý này ok rồi nhé :> Mà sao ko thấy kí hiệu "ko thuộc" nhờ :v
Hình như tui nhấn Shift+Enter nên nó ko nhảy dòng rồi -.- Thôi kệ đi, bạn xem tạm nhé

Đặt : \(\overrightarrow{BA}=\overrightarrow{a},\overrightarrow{BB'}=\overrightarrow{b,}\overrightarrow{BC}=\overrightarrow{c}\)
Ta có : \(\overrightarrow{BD'}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Do MM//BD' nên tồn tại số thực k sao cho \(\overrightarrow{MN}=k\overrightarrow{BD'}\)
hay :
\(\overrightarrow{MN}=k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}\) (1)
Đặt
\(\frac{MC}{AC}=x,\frac{C'N}{C'D}=y;x,y\in\left(0;1\right)\)
Ta có :
\(\overrightarrow{AC}=\overrightarrow{c}-\overrightarrow{a,}\overrightarrow{C'D}=\overrightarrow{a}-\overrightarrow{b,}\)
Suy ra : \(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CC'}+\overrightarrow{C'N}\)
\(=\overrightarrow{xAC}+\overrightarrow{CC'}+\overrightarrow{yC'N}\)
\(=x\left(\overrightarrow{c}-\overrightarrow{a}\right)+\overrightarrow{b}+y\left(\overrightarrow{a}-\overrightarrow{b}\right)\)
\(=\left(y-x\right)\overrightarrow{a}+\left(1-y\right)\overrightarrow{b}+x\overrightarrow{c}\) (2)
Từ (1) và (2) suy ra :
\(k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}=\left(y-x\right)\overrightarrow{a}+\left(1-y\right)\overrightarrow{b}+x\overrightarrow{c}\)
\(\Leftrightarrow\left(k+x-y\right)\overrightarrow{a}+\left(k+y-1\right)\overrightarrow{b}+\left(k-x\right)\overrightarrow{c}=\overrightarrow{0}\) (3)
Do \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) không đồng phửng nên (3) tương đương với
\(\begin{cases}k+x-y=0\\k+y-1=0\\k-x=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=\frac{1}{3}=k\\y=\frac{2}{3}\end{cases}\)
Vậy với \(3\overrightarrow{MC}=\overrightarrow{AC,}3\overrightarrow{C'N}=2\overrightarrow{C'D}\)
thì MN//BD' và khi đó \(\frac{MN}{BD'}=\frac{1}{3}\)

- Tìm ảnh của điểm Q qua phép tịnh tiến theo \(\overrightarrow{CD}=\overrightarrow{U}=\overrightarrow{QQ'}\)
Khi đó MN=QQ’ , suy ra MQ=NQ’ . Cho nên PN+MQ=PN+NQ’ ngắn nhất khi P,N,Q’ thẳng hàng .
- Các bước thực hiện :
+/ Tìm Q’ sao cho : \(\overrightarrow{CD}=\overrightarrow{U}=\overrightarrow{QQ'}\)
+/ Nối PQ’ cắt AD tại điểm N
+/ Kẻ NM //CD cắt BC tại M . Vậy tìm được M,N thỏa mãn yêu cầu bài toán .
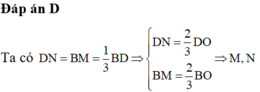


Ta cần chứng minh \(\overrightarrow{MN}.\overrightarrow{AM}=0\)
Đặt \(\frac{BM}{MH}=\frac{CN}{ND}=k\), khi đó \(\overrightarrow{MB=}-k\overrightarrow{MH}\) , \(\overrightarrow{NC=}-k\overrightarrow{ND}\)
Suy ra \(\left(1+k\right)\overrightarrow{AM}=\overrightarrow{AB}+k\overrightarrow{AH}\)
và \(\left(1+k\right)\overrightarrow{MN}=\overrightarrow{BC}+k\overrightarrow{HD}\)
Suy ra :
\(\left(1+k\right)^2\overrightarrow{MN}.\overrightarrow{AM}=k\left(\overrightarrow{AB}.\overrightarrow{HD}+\overrightarrow{AH}.\overrightarrow{BC}\right)\)
\(=k\left(\overrightarrow{HB}.\overrightarrow{HD}+\overrightarrow{AH}.\overrightarrow{BC}\right)\)
\(=k\left(\overrightarrow{-AH^2}+\overrightarrow{AH}.\overrightarrow{AD}\right)\)
\(=k\overrightarrow{AH}.\overrightarrow{HD}=0\)
Suy ra điều phải chứng minh