Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
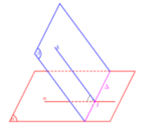
Phương pháp:
Xác định góc giữa hai mặt phẳng 
- Tìm giao tuyến
∆
của 
- Xác định 1 mặt phẳng 
- Tìm các giao tuyến 
- Góc giữa hai mặt phẳng 
Cách giải:
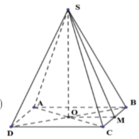
Gọi M là trung điểm của BC. Ta có:
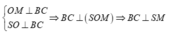
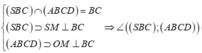
ABCD là hình vuông cạnh a
∆ SOB vuông tại O
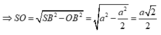
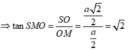
Chọn: A
Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
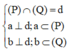
khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Sử dụng định lý hàm số cos trong tam giác để tính toán:
Cho tam giác ABC khi đó 
Cách giải:
Hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, ta tìm góc giữa hai mặt phẳng (SAD) và (SBC).
Gọi M, N là trung điểm các cạnh AD và BC, khi đó SM ⊥ AD và SN ⊥ BC (do các tam giác SBC;SAD là các tam giác đều).
Vì BC//AD nên giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng d qua S và song song AD, BC.
Vì SM
⊥
AD và SN
⊥
BC nên SM
⊥
d và SN
⊥
d mà 
góc giữa hai mặt phẳng (SAD) và (SBC) là góc MSN.
Mặt bên là các tam giác đều cạnh a nên 
Khi đó: 
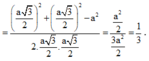
Chọn A
Chú ý khi giải:
Các em có thể tính SO theo tỉ số lượng giác và suy ra MSN = 2MSO
Chọn D.
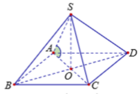
Theo giả thiết S.ABCD là hình chóp tứ giác đều có tất cả các cạnh bằng nhau nên đặt AB = a => SB = a.
Gọi O là tâm của hình vuông ABCD thì 
Xét tam giác SAO vuông tại O có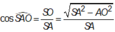 
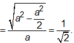
Đáp án A
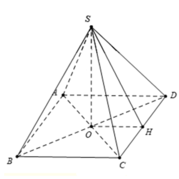
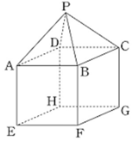
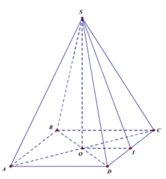
Gọi O là tâm hình vuông ABCD, M là trung điểm CD.
Khi đó SO là đường cao hình chóp, góc SMO là góc giữa mặt bên và mặt đáy của hình chóp.
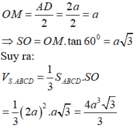
Chọn A
Phương pháp:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải
Đáp án A.
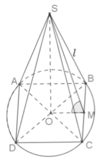
Gọi M là trung điểm của BC, suy ra:
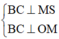
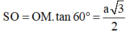
Gọi l, R lần lượt là đường sinh và bán kính của hình nó ngoại tiếp hình chóp, khi đó:
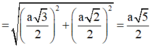
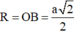
Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:
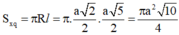
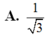
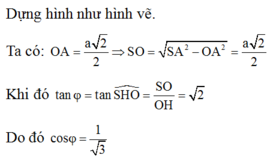
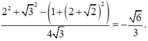
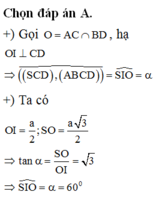
Chọn A.
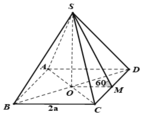
H là trung điểm CD
Ta có: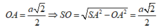
Khi đó: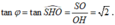
Do đó