Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
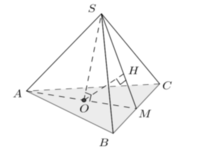
- Gọi O là trọng tâm của tam giác ABC và M là trung điểm của BC.
- Vì hình chóp S.ABC là hình chóp tam giác đều nên: S) ⊥ (ABC); SO = a√3.
- Kẻ OH ⊥ SM, ta có:
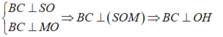 nên suy ra d(O; (SBC)) = OH.
nên suy ra d(O; (SBC)) = OH.
- Ta có:
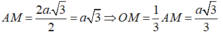
- Xét tam giác vuông SOM, đường cao OH có:
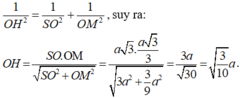

Chọn đáp án B

Gọi G là trọng tâm tam giác đều ABC, E là trung điểm của SA, K, H là hình chiếu của G, E lên SA.
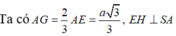
HE ⊥ BC vì HE là trung tuyến trong tam giác cân HBC.
Suy ra HE là đoạn vuông góc chung của SA và BC
![]()
Xét tam giác SAG vuông tại G. SG = tan 60 0 .AG = a
![]()


Gọi \(I\) là trung điểm của \(BC\), kẻ \(OH \bot SI\left( {H \in SI} \right)\).
\(ABC\) là tam giác đều \( \Rightarrow AI \bot BC\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot BC\)
\( \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot OH\)
Mà \(OH \bot SI\)
\( \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)
\(ABC\) là tam giác đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow OI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{3}\)
\(SO = a\sqrt 2 \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {14} }}{7}\)
Chọn A.

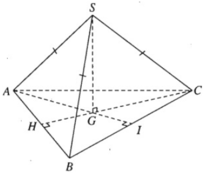
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
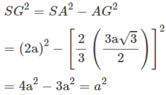
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
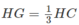
mà 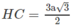
nên 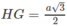
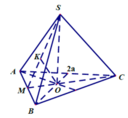
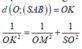
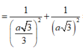
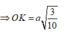
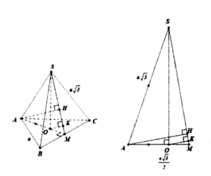

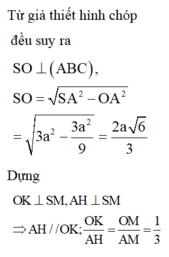


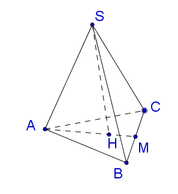
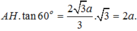
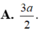
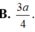
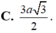
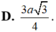
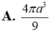
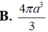
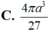
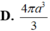
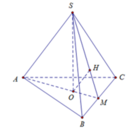
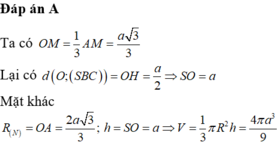


- Vì hình chóp S.ABC đều có SO là đường cao ⇒ O là tâm của Δ ABC.
- Gọi I là trung điểm cạnh BC. Tam giác ABC đều nên:
- Xét tam giác SOA vuông tại O :