Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích đáy lớn là: \(S = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Diện tích đáy bé là: \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}\left( {{a^2}\sqrt 3 + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} + \frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{7\sqrt 2 }}{{12}}{a^3}\)
Chọn C.

Chọn C.
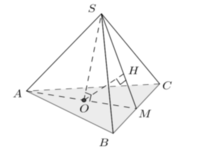
- Gọi O là trọng tâm của tam giác ABC và M là trung điểm của BC.
- Vì hình chóp S.ABC là hình chóp tam giác đều nên: S) ⊥ (ABC); SO = a√3.
- Kẻ OH ⊥ SM, ta có:
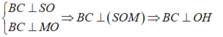 nên suy ra d(O; (SBC)) = OH.
nên suy ra d(O; (SBC)) = OH.
- Ta có:
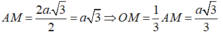
- Xét tam giác vuông SOM, đường cao OH có:
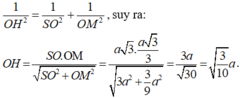

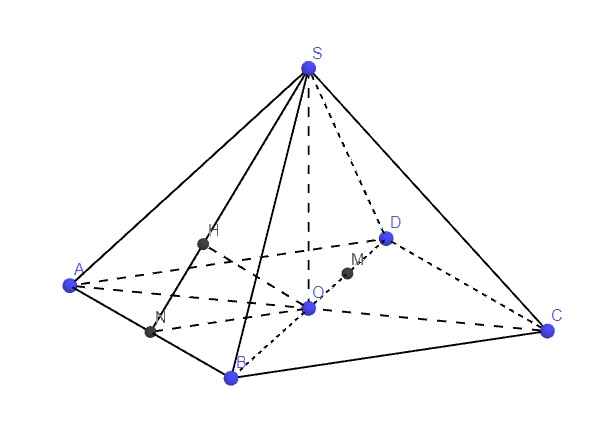
Gọi N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}ON\perp AB\\SO\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SON\right)\)
Từ O kẻ \(OH\perp SN\) (H thuộc SN) \(\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(ON=\dfrac{1}{2}AD=\dfrac{a}{2}\) ; \(SO=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{6}}{6}\)
Lại có: M là trung điểm OD \(\Rightarrow OM=\dfrac{1}{2}OD\Rightarrow BM=\dfrac{3}{2}OB\)
\(\Rightarrow d\left(M;\left(SAB\right)\right)=\dfrac{3}{2}d\left(O;\left(SAB\right)\right)=\dfrac{3}{2}.\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{4}\)

\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)
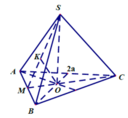
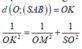
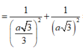
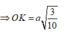
Gọi \(I\) là trung điểm của \(BC\), kẻ \(OH \bot SI\left( {H \in SI} \right)\).
\(ABC\) là tam giác đều \( \Rightarrow AI \bot BC\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot BC\)
\( \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot OH\)
Mà \(OH \bot SI\)
\( \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)
\(ABC\) là tam giác đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow OI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{3}\)
\(SO = a\sqrt 2 \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {14} }}{7}\)
Chọn A.