Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(I\) là trung điểm của \(BC\), kẻ \(OH \bot SI\left( {H \in SI} \right)\).
\(ABC\) là tam giác đều \( \Rightarrow AI \bot BC\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot BC\)
\( \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot OH\)
Mà \(OH \bot SI\)
\( \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)
\(ABC\) là tam giác đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow OI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{3}\)
\(SO = a\sqrt 2 \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {14} }}{7}\)
Chọn A.

Diện tích mặt đáy là:\(\dfrac{a^2.\sqrt{3}}{4}\)
Thể tích khối lăng trụ là: \(a.\dfrac{a^2.\sqrt{3}}{4}=\dfrac{a^3.\sqrt{3}}{4}\)
\(\Rightarrow A\)

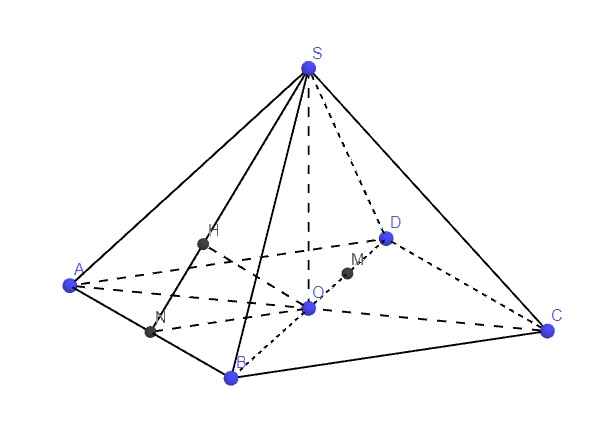
Gọi N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}ON\perp AB\\SO\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SON\right)\)
Từ O kẻ \(OH\perp SN\) (H thuộc SN) \(\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(ON=\dfrac{1}{2}AD=\dfrac{a}{2}\) ; \(SO=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{6}}{6}\)
Lại có: M là trung điểm OD \(\Rightarrow OM=\dfrac{1}{2}OD\Rightarrow BM=\dfrac{3}{2}OB\)
\(\Rightarrow d\left(M;\left(SAB\right)\right)=\dfrac{3}{2}d\left(O;\left(SAB\right)\right)=\dfrac{3}{2}.\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{4}\)

\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)


Gọi \(O,O'\) lần lượt là tâm của hai đáy \(ABC\) và \(A'B'C'\), \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\).
Kẻ \(A'H \bot AO\left( {H \in AO} \right) \Rightarrow A'H = OO'\)
\(\Delta ABC\) đều \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
\(\Delta A'B'C'\) đều \( \Rightarrow A'M' = \frac{{\frac{a}{2}.\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4} \Rightarrow A'O' = \frac{2}{3}A'M' = \frac{{a\sqrt 3 }}{6}\)
\(A'HOO'\) là hình chữ nhật \( \Rightarrow OH = A'O' = \frac{{a\sqrt 3 }}{6}\)
\( \Rightarrow AH = AO - OH = \frac{{a\sqrt 3 }}{6}\)
Tam giác \(AA'H\) vuông tại \(H\)
\( \Rightarrow OO' = A'H = \sqrt {AA{'^2} - A{H^2}} = \frac{{a\sqrt {141} }}{6}\)
Diện tích đáy lớn là: \(S = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Diện tích đáy bé là: \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}\left( {{a^2}\sqrt 3 + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} + \frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{7\sqrt 2 }}{{12}}{a^3}\)
Chọn C.