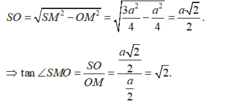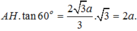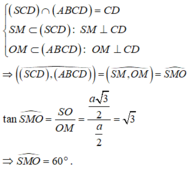Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

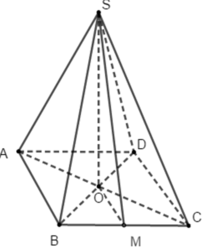
Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
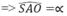
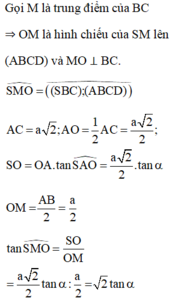
Đáp án C

Lời giải:
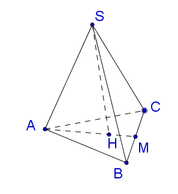
$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$
Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$
Do đó:
$\angle ((SBC), (ABC))=\angle (SM, HM)$
$=\widehat{SMH}=60^0$
$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$
$\Rightarrow SH=\sqrt{3}HM$
Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$
Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$

Gọi O là tâm đáy, M là trung điểm AB
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy
\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)
\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)

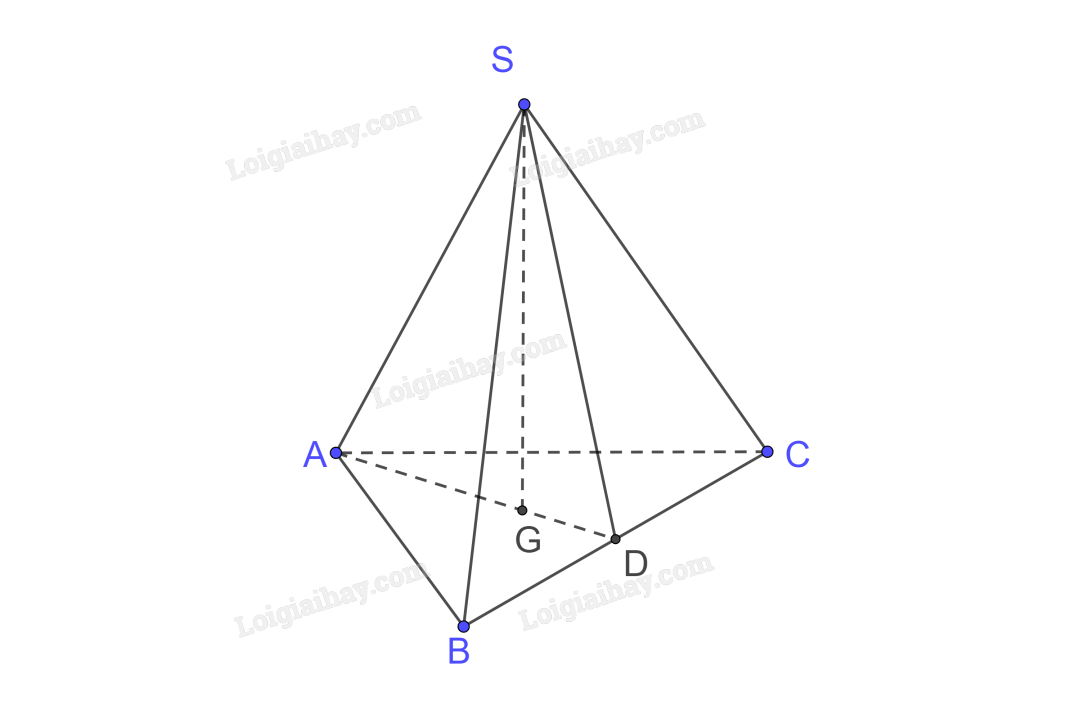
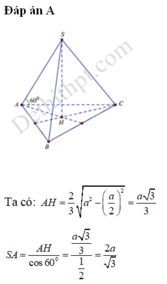
Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.
Gọi AG cắt BC tại D
a) Ta có A là hình chiếu của A trên (ABC)
G là hình chiếu của S trên (ABC)
\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)
\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác SAG vuông tại G có
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)
b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(BC \bot AD\) (G là trực tâm)
\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)
Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)
Xét tam giác SGD vuông tại G có
\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)

Ta tính được \(AG=a\dfrac{\sqrt{3}}{3}\)
Từ gt ta có:
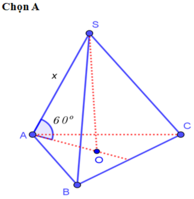
\(\widehat{\left(SA,\left(ABC\right)\right)}=\widehat{\left(SA,AG\right)}=\widehat{SAG}=60^0\)(Vì S.ABC là chóp tam giác đều nên \(SG\perp\left(ABC\right)\))
Khi đó SG=AG.tan60=a
Gọi M là trung điểm BC \(\Rightarrow GM=a\dfrac{\sqrt{3}}{6}\)
Đặt d(G,(SBC))=x
Áp dụng mô hình "điểm tốt - vẽ hai bước" cho hình chóp S.GBC với G là "điểm tốt" ta có:
\(\dfrac{1}{x^2}=\dfrac{1}{SG^2}+\dfrac{1}{GM^2}=\dfrac{1}{a^2}+\dfrac{1}{\left(a\dfrac{\sqrt{3}}{6}\right)^2}\)
\(\Rightarrow x=\dfrac{a}{\sqrt{13}}\)
Mô hình "điểm tốt - vẽ hai bước": Cho hình chóp S.ABC với \(SA\perp\left(ABC\right)\). Kẻ \(AH\perp BC,AK\perp SH\) thì d(A,(SBC))=AK.
CM: Ta có: \(SA\perp\left(ABC\right)\Rightarrow SA\perp AH\)
Mà \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\)
\(\Rightarrow\left(SBC\right)\perp\left(SAH\right)\) theo giao tuyến SH
Mà \(AK\perp SH,AK\subset\left(SAH\right)\) \(\Rightarrow AK\perp\left(SBC\right)\), dễ dàng suy ra đpcm

Đáp án A.
- Phương pháp:
+) Xác định góc giữa mặt bên và đáy là góc giữa hai đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng đó.
+) Tính tan của góc xác định được.
Cách giải:
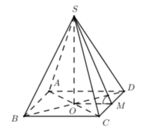
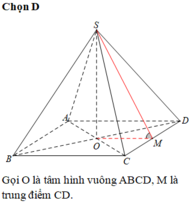
- Gọi O = AC ∩ BD. Do S.ABCD là chóp đều ⇒ SO ⊥ (ABCD).
- Gọi M là trung điểm của CD ta có: OM là đường trung bình của tam giác BCD ⇒ OM // BC ⇒ OM ⊥ CD.
- Ta có:

- Áp dụng định lý Pytago trong tam giác vuông SOM ta có: