Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
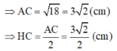
Lại có: SH2 = SC2 - HC2 (Pytago)
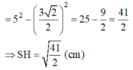
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
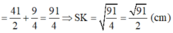
![]()
![]()
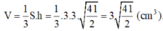

Lời giải:
Xét tam giác $SAB$ có $SA=SB=10$, $AB=12$
Kẻ $SH\perp AB$ thì $H$ là trung điểm của $AB$.
$\Rightarrow AH=6$ (cm)
Theo định lý Pitago:
$SH=\sqrt{SA^2-AH^2}=\sqrt{10^2-6^2}=8$ (cm)
$S_{SAB}=\frac{SH.AB}{2}=\frac{8.12}{2}=48$ (cm vuông)
$S_{xq}=3S_{SAB}=3.48=144$ (cm vuông)

a) Chân đường cao H của hình chóp S.ABC trùng với trọng tâm của tam giác ABC.
Gọi M là trung điểm của BC
Tam giác ABC có
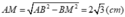
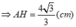
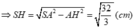
b) Tam giác SAM cân ở M nên
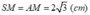
Diện tích xung quanh của hình chóp:
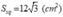
c) Diện tích toàn phần của hình chóp:
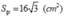
d) Thể tích của hình chóp
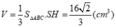
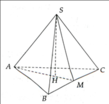

a) Áp dụng định lý Pytago, ta được:
AC2=AB2+BC2=2AB2AC2=AB2+BC2=2AB2
⇒AC=AB√2=10√2cm⇒AC=AB2=102cm
b) Gọi MM là trung điểm ABAB
⇒MA=MB=MO=5cm⇒MA=MB=MO=5cm
⇒SM⊥AB⇒SM⊥AB (ΔSAB∆SAB cân tại SS)
⇒SM=√SA2−AM2=√122−52=√119cm⇒SM=SA2−AM2=122−52=119cm
⇒SO=√SM2−OM2=√119−52=√94cm⇒SO=SM2−OM2=119−52=94cm
⇒VS.ABCD=13.SABCD.SO=13.AB2.SO=102.943=94003cm3

Thể tích của hình chóp đều là:
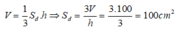
Gọi độ dài cạnh đáy là a.
Do đáy là tam giác đều nên diện tích đáy là:
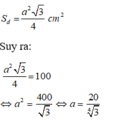
Chọn đáp án D

a: \(AC=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\)
b: AO=5căn 2(cm)
=>\(SO=\sqrt{SA^2+AO^2}=\sqrt{194}\left(cm\right)\)