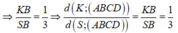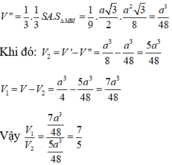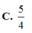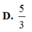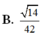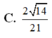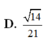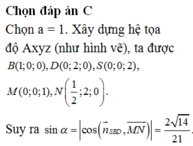Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
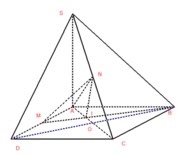
Coi hình chóp AMNI với điểm N làm đỉnh và AMI làm đáy
+) Từ N là trung điểm của SC nên đường cao
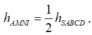
+) Lấy O là tâm hình chữ nhật ta có BM, AO là các trung tuyến nên I là trọng tâm tam giác ABD nên
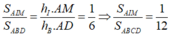
+) Suy ra
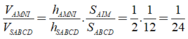

Chọn B
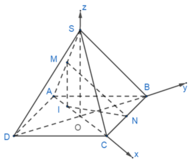
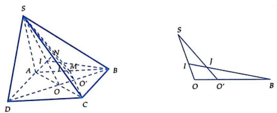
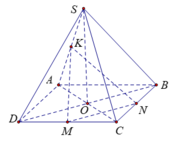
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
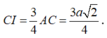
Xét tam giác CNI có
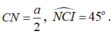
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
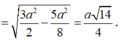
Mà MI//SO
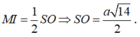
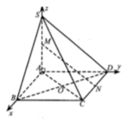
Chọn hệ trục tọa độ như hình vẽ. Ta có:
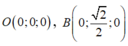
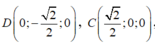
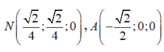
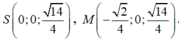
Khi đó
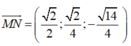
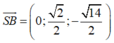
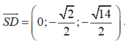
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
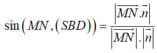
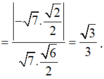

Phương pháp:
Xác định chiều cao hình chóp bằng kiến thức 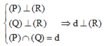
Xác định khoảng cách ![]()
Tính toán bằng cách sử dụng quan hệ diện tích, định lý hàm số cosin, công thức tính diện tích tam giác S =
1
2
a.h với a là cạnh đáy, h là chiều cao tương ứng và ![]()
Cách giải:
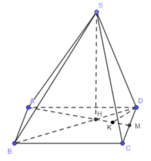
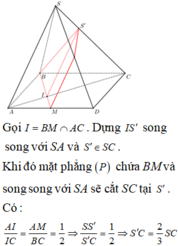
Gọi H = AM ∪ BD
Ta có 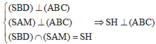
Vì AB//CD nên theo định lý Ta-lét ta có

Ta có ![]()
![]()
![]()
Vì M là trung điểm của DC và ABCD là hình bình hành có diện tích 2 a 2 nên ta có:
![]()
Lại có CD = AB = a
2
![]()
Khi đó ![]()
![]()
![]()
![]()
![]()
![]()
Lại có ![]()
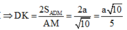
Từ đó ![]()
Chọn: C

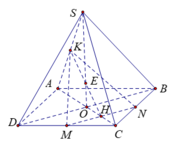
Gọi I là chân đường vuông góc kẻ từ H lên SC
Vì MD ⊥ (SCN), MD ∩ (SCN) = H nên
d(MD, SC) = d(H, SC) = HI = HC.sin60
°
= 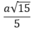

Chọn đáp án D
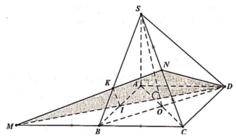
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 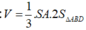
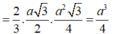
Ta có: N là trung điểm SC nên 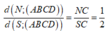
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC