Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Ta có: ![]() (chiều cao của hình chóp)
(chiều cao của hình chóp)
Diện tích hình vuông ![]()
Thể tích khối chóp SABCD là: 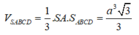

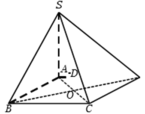
a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)

Bạn chỉ nên đăng 1 bài 1 lần thôi, tránh làm loãng box toán!

Lời giải:
Vì $SA\perp (ABCD)$ nên
$60^0= \angle (SC, (ABCD))=\angle (SC, AC)=\widehat{SCA}$
Ta có:
$AC=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
$\frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{15}a$
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}$
$=\frac{1}{3}.\sqrt{15}a.a.2a=\frac{2\sqrt{15}}{3}a^3$

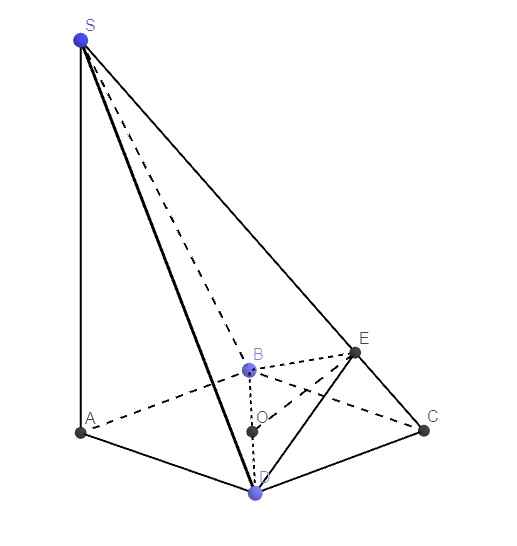
a/ Kẻ \(CE//BD\Rightarrow BD//\left(SCE\right)\Rightarrow d\left(SC,BD\right)=d\left(BD,\left(SCE\right)\right)=d\left(B,\left(SCE\right)\right)\)
\(AB\cap\left(SCE\right)=\left\{E\right\}\Rightarrow\dfrac{d\left(B,\left(SCE\right)\right)}{d\left(A,\left(SCE\right)\right)}=\dfrac{EB}{EA}=\dfrac{1}{2}\)
\(\widehat{CAE}=\dfrac{1}{2}\widehat{DAB};\widehat{AEC}=\widehat{BDC}=\dfrac{1}{2}\widehat{ADC};\widehat{DAB}+\widehat{ADC}=180^0\Rightarrow\widehat{CAE}+\widehat{AEC}=90^0\Rightarrow\widehat{ACE}=90^0\)
\(\Rightarrow AC\perp EC\)
\(\left\{{}\begin{matrix}SA\perp CE\\AC\perp CE\end{matrix}\right.\Rightarrow CE\perp\left(SAC\right)\Rightarrow\left(SCE\right)\perp\left(SAC\right)\)
Kẻ \(AH\perp SC\Rightarrow AH\perp\left(SCE\right)\Rightarrow d\left(A,\left(SCE\right)\right)=AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=..\)
\(\Rightarrow d\left(SC,BD\right)=d\left(B,\left(SCE\right)\right)=\dfrac{AH}{2}=...\)
b/ \(AD//BC\Rightarrow AD//\left(SBC\right)\Rightarrow d\left(SC,AD\right)=d\left(AD,\left(SBC\right)\right)=d\left(A,\left(SBC\right)\right)\)
Kẻ \(AK\perp BC\Rightarrow\left\{{}\begin{matrix}SA\perp BC\\AK\perp BC\end{matrix}\right.\Rightarrow\left(SBC\right)\perp\left(SAK\right)\)
Kẻ \(AM\perp SK\Rightarrow AM\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AM=\dfrac{SA.AK}{\sqrt{SA^2+AK^2}}=...=d\left(SC,AD\right)\)

\(\left\{{}\begin{matrix}BD\perp AC\left(\text{ABCD là hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow BD\in\left(\alpha\right)\)
Trong mp (SBC), từ B kẻ \(BE\perp SC\Rightarrow E\in\left(\alpha\right)\)
\(\Rightarrow\) Tam giác BDE là thiết diện của chóp và \(\left(\alpha\right)\)
\(BD=AB\sqrt{2}=a\sqrt{2}\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) hay tam giác SBC vuông tại B
\(SB=\sqrt{SA^2+AB^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{BE^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}-\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BE=DE=\dfrac{2a\sqrt{5}}{5}\)
\(\Rightarrow OE=\sqrt{BE^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{30}}{10}\)
\(S_{BDE}=\dfrac{1}{2}OE.BD=\dfrac{a^2\sqrt{15}}{10}\)

Chọn đáp án A
Đường chéo hình vuông AC = 2
Xét tam giác SAC, ta có
![]()
Chiều cao của khối chóp là SA = 3
Diện tích hình vuông ABCD là
![]()
Thể tích khối chóp S. ABCD là


Kẻ SH vuông góc AB tại H.
a, Ta có: \(h=SH=AH.tan\alpha=2a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.2a=\dfrac{8a^3}{3}\)
b, \(SB=BC.tan\alpha=2\sqrt{5}a\Rightarrow SH=\sqrt{SB^2-BH^2}=\sqrt{19}a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.\sqrt{19}a=\dfrac{4\sqrt{19}a^3}{3}\)
c, Kẻ HI vuông góc với CD.
Ta có: \(SH=HI.tan\alpha=6a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.6a=8a^3\)



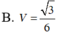
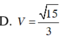
Có \(AC=AD\sqrt{2}=a\sqrt{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\) \(\Rightarrow\Delta SAC\) vuông tại A.
\(\Rightarrow SA=\sqrt{SC^2-AC^2}=\sqrt{\left(a\sqrt{3}\right)^2-\left(a\sqrt{2}\right)^2}=a\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.S_{ABCD}.SA=\dfrac{1}{3}.AD^2.SA=\dfrac{1}{3}.a^2.a=\dfrac{a^3}{3}\)