Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
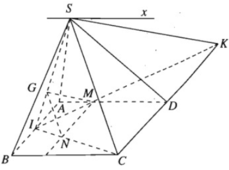
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
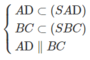
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
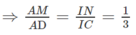
Mà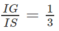 
(G là trọng tâm của ∆SAB) nên
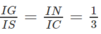⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
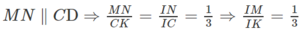
Ta có:
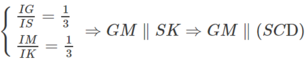
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà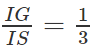 
(G là trọng tâm của ∆SAB) nên
⇒ GN // SC
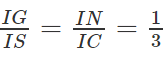
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:
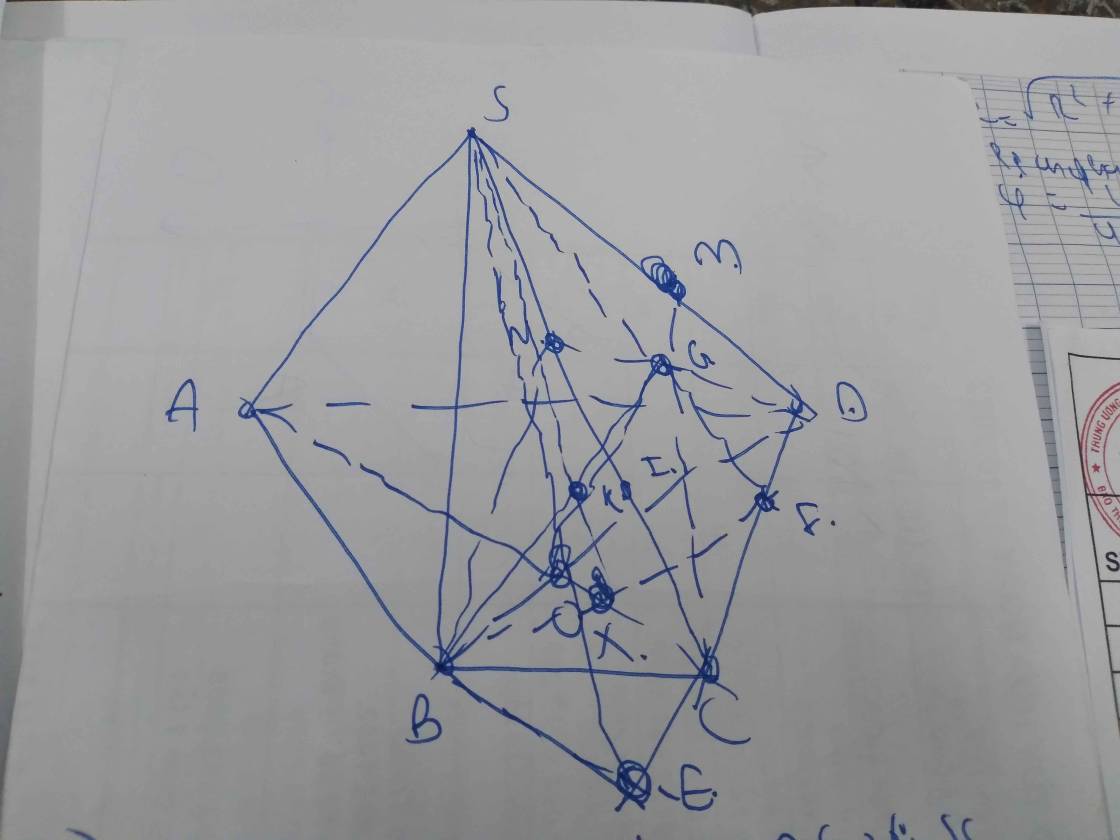
Trong mp(SAB), gọi M là giao điểm của SG với AB
Trong mp(SBC), gọi N là giao điểm của SO với BC
Xét ΔSAB có
G là trọng tâm
M là giao điểm của SG với AB
Do đó: M là trung điểm của AB
=>\(SG=\dfrac{2}{3}SM\)
Xét ΔSBC có
O là trọng tâm
SO cắt BC tại N
Do đó: N là trung điểm của BC
=>\(SO=\dfrac{2}{3}SN\)
Xét ΔSMN có \(\dfrac{SG}{SM}=\dfrac{SO}{SN}=\dfrac{2}{3}\)
nên GO//MN
GO//MN
\(MN\subset\left(ABC\right)\)
GO không thuộc mp(ABC)
Do đó: GO//(ABC)
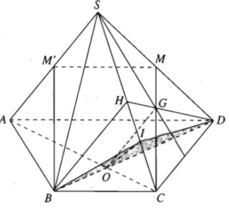
a) Gọi H là trung điểm của SC
Ta có:
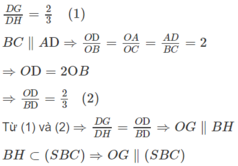
b) Gọi M’ là trung điểm của SA ⇒ MM′ // AD và MM′ = AD/2.
Mặt khác vì BC // AD và BC = AD/2 nên BC // MM′ và BC = MM′.
Do đó tứ giác BCMM’ là hình bình hành ⇒ CM // BM′ mà BM′ ⊂ (SAB)
⇒ CM // (SAB)
c) Ta có: 
Mặt khác vì 
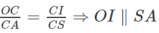
OI ⊂ (BID) ⇒ SA // (BID)
Bạn coi lại đề bài.
N,M,P,Q là các điểm trên CD, AD, SA hay trung điểm?
Vì nếu trung điểm thì làm sao thỏa mãn MD=2MC hay NA=3ND được?
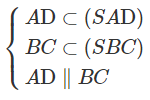
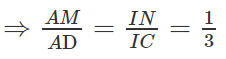
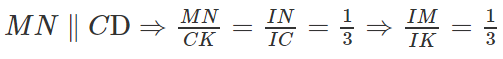
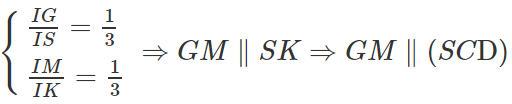
a) Ta có SM = MN = NA và G là trọng tâm của tam giác ABC. Khi đó, ta có:
SG = 2GM (vì G là trọng tâm)
SG = 2GN (vì G là trọng tâm)
Vậy GM = GN
Do đó, ta có tam giác SMN là tam giác đều.
Vì SM = MN = NA, nên tam giác SNA cũng là tam giác đều.
Từ đó, ta có góc SNA = 60°.
Mà góc SNA = góc SNB + góc BNA = góc SNB + góc BNC.
Vậy góc SNB + góc BNC = 60°.
Nhưng góc SNB + góc BNC = góc SBC.
Vậy góc SBC = 60°.
Do đó, GM // (SBC).
b) Gọi D là điểm đối xứng của A qua G.
Ta có GD = GA (vì D là điểm đối xứng của A qua G)
Và GM = GN (vì G là trọng tâm)
Vậy tam giác GDM và tam giác GAN là tam giác đồng dạng (cạnh bằng nhau và góc bằng nhau).
Từ đó, ta có góc GDM = góc GAN.
Nhưng góc GDM = góc MCD và góc GAN = góc NGB.
Vậy góc MCD = góc NGB.
Do đó, (MCD) // (NBG).
c) Gọi H = DM ∩ (SBC).
Ta cần chứng minh H là trọng tâm của tam giác SBC.
Vì G là trọng tâm của tam giác ABC, nên AG = 2GM.
Và GD = GA (vì D là điểm đối xứng của A qua G).
Từ đó, ta có AD = 2GD.
Vậy D là trọng tâm của tam giác AGD.
Do đó, DH là đường cao của tam giác AGD.
Vậy DH cắt AG tại I sao cho AI = 2IG.
Mà AI = 2IG nên I là trọng tâm của tam giác AGD.
Vậy I nằm trên đường thẳng DM.
Từ đó, ta có H = DM ∩ (SBC) là trọng tâm của tam giác SBC.
Vậy H là trọng tâm của tam giác SBC.