Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Gọi H là trung điểm của BC khi đó S H ⊥ B C do S B C ⊥ A B C ⇒ S H ⊥ A B C
Lại có: C B = 2 C H ⇒ d C ; S A B = 2 d H ; S A B
Dựng H E ⊥ A B H F ⊥ S E ⇒ d H = H F
Mặt khác H E = A C 2 = 1 2 B C . sin A B C ^ = a 4 ; S H = a 3 2
Do đó H F = S H . H E S H 2 + H E 2 = a 39 26 ⇒ d c = a 39 13

Đáp án C
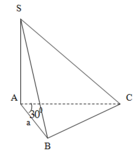
B C = A B . tan 30 0 = a 3 3 ⇒ A C = a 2 3 + a 2 = 2 3 3 a V = 1 3 . S A . 1 2 . A B . B C = 1 3 . S A . 1 2 . a . a 3 3 = a 3 3 36 ⇒ S A = a 2 S B = a 2 4 + a 2 = a 5 2 V = 1 3 . d ( A ; S B C ) . 1 2 . S B . B C = 1 3 . d . 1 2 . a 5 2 . a 3 3 = a 3 3 36 ⇒ d = a 5 5

Đáp án C
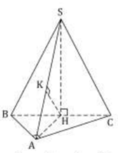

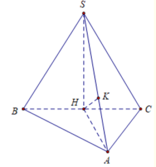
Từ (1), (2) => HK là đoạn vuông góc chung của SA và BC

Tam giác SHA vuông tại A có đường cao HK nên 1 HK 2 = 1 SH 2 + 1 AH 2 = 4 3 a 2 + 4 a 2 = 16 3 a 2 .
⇒ HK = 3 a 4 .

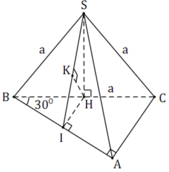
Ta có A I ⊥ B C , S A ⊥ B C
Suy ra V = a 3 , S ∆ A B C = a 2 3 4 ⇒ S A = 4 a 3
Mà A I = a 3 2
Trong tam giác vuông ∆ S A I ta có 1 A K 2 = 1 A S 2 + 1 A I 2 Vậy d = A K = A S 2 . A I 2 A S 2 + A I 2 = 4 a 195 65
Đáp án C

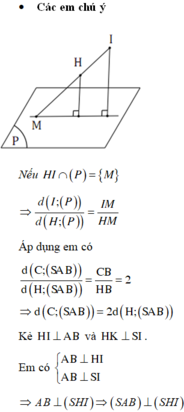

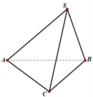

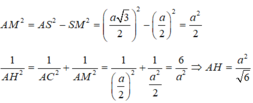
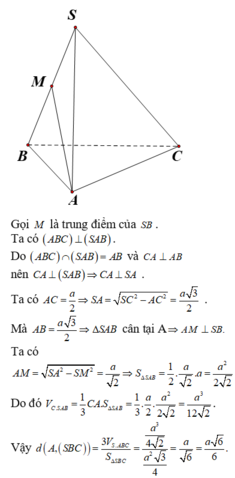
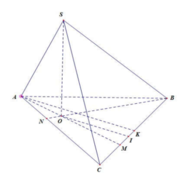

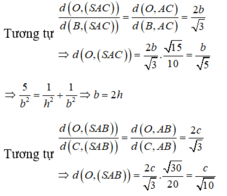
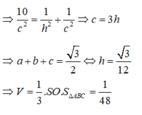

Chọn C.
Phương pháp:
Đưa về dựng khoảng cách từ M đến (SAB) với M là trung điểm của BC.
Cách giải:
Gọi M, N lần lượt là trung điểm của BC, AB.