Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 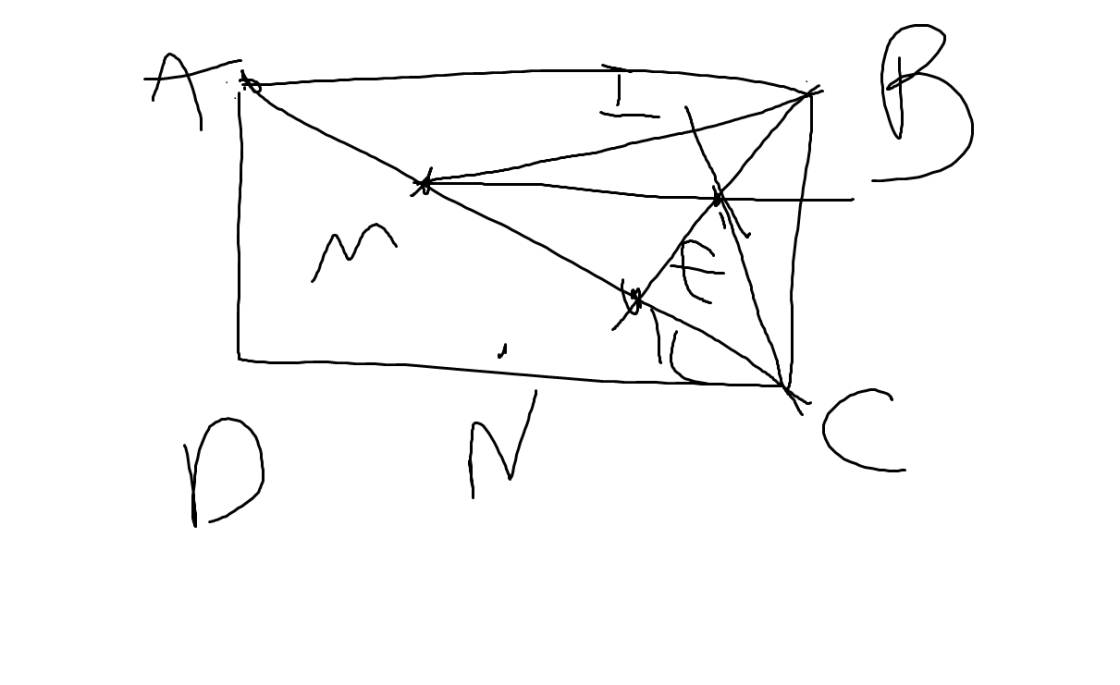
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB

a, Xét tg AHD và tg CIB có \(AD=BC;\widehat{AHD}=\widehat{CIB}=90^0;\widehat{ADH}=\widehat{CBI}\left(so.le.trong\right)\) nên \(\Delta AHD=\Delta CIB\left(ch-gn\right)\)
Do đó \(AH=CI\)
Mà AH//CI (⊥BD) nên AHCI là hbh
b, Vì AHCI là hbh mà M là trung điểm HI nên cũng là trung điểm AC
Do đó A đối xứng C qua M

a: Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hình bình hành
b: DH đi qua A
mà AH vuông góc BC(2)
nên DH vuông góc BC
DH đi qua A
mà DH cắt BC tại trung điểm của BC
nên AH cắt BC tại trung điểm của BC(1)
Từ (1), (2) suy ra ΔABC cân tại A

a: Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hình bình hành
b: Xét ΔAKB vuông tại K và ΔAIC vuông tại I có
góc KAB chung
=>ΔAKB đồng dạng với ΔAIC
=>AK/AI=AB/AC
=>AK*AC=AB*AI; AK/AB=AI/AC
c: Xét ΔAKI và ΔABC có
AK/AB=AI/AC
góc KAI chung
=>ΔAKI đồng dạng với ΔABC