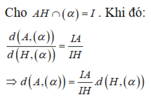Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(xin lỗi vì mình không biết chèn hình, các bạn chịu khó tự vẽ. Cảm ơn ạ)
Gọi O là giao điểm 2 đường chéo
I là trung điểm BK
H là trung điểm BE
Xét tam giác(tg) BKD có
I là trung điểm BK
O là trung điểm BD
=>OI là đường trung bình của tgBKD
=> OI // KD
=> OI \(\perp\)BK
Lại có I là trung điểm BK
=> O \(\in\)đường trung trực của BK
*Tương tự ta sẽ chứng minh được O \(\in\)đường trung trực của BE
Từ đó suy ra O là trực tâm của tgBKE
Ta có BO = BD:2
<=> BO = \(\frac{5}{2}\)
Vậy...
Done~

a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ

Tam giác ABC vuông tại A, ta tính được AC:
\(AC^2=BC^2-AB^2=25a^2-9a^2=16a^2\Rightarrow AC-4a\)
Trong mặt phẳng (SAC), qua S kẻ SH vuông góc với AC, H thuộc ACTa có:\(SH=SA.sin30^0=2a\sqrt{3}.\frac{1}{2}=a\sqrt{3}\)\(AH=SA.cos30^0=2a\sqrt{3}.\frac{\sqrt{3}}{2}=3a\)Thể tích khối chóp S.ABC: \(V_{S.ABC}=\frac{1}{2}.SH.S_{\Delta ABC}=\frac{1}{3}.a\sqrt{3}.\frac{1}{2}.3a.4a=2\sqrt{3}a\)Trong mặt phẳng đáy (ABC), qua H kẻ HK vuông góc với BC và cắt BC tại KTam giác HKC đồng dạng với tam giác BAC, ta được:\(\frac{HK}{AB}=\frac{HC}{BC}=\frac{a}{5a}=\frac{1}{5}\rightarrow HK=\frac{1}{5}AB=\frac{1}{5}.3a=\frac{3}{5}a\)Nối SK. Trong mặt phẳng (SHK), từ H kẻ HI vuông góc với SKTa chứng minh được HI vuông góc với mặt phẳng (SBC):Ta có:\(\begin{cases}HK\perp BC\\BC\perp SH\end{cases}\Rightarrow BC\perp\left(SHK\right)\Rightarrow BC\perp HI\)mặt khác: BC_|_HI (1)
HI_|_SK(2)từ (1) (2)=> HI_|_(SBC)Khoảng cách từ điểm H đến mặt phẳng (ABC) là HIXác định khoảng cách từ A đến mặt phẳng (ABC)Suy ra khoảng cách từ A đến mặt phẳng (SBC) được tính theo:

a.
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\) \(\Rightarrow SH\perp CD\)
Gọi E là trung điểm CD \(\Rightarrow HE||BC\Rightarrow HE\perp CD\)
\(\Rightarrow CD\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a), \(HE=BC=a\)
Hệ thức lượng: \(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Do \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=\dfrac{a\sqrt{21}}{7}\)
b.
Theo tính chất trọng tâm, ta có \(GS=\dfrac{2}{3}HS\)
Mà \(HG\cap\left(SCD\right)=S\Rightarrow d\left(G;\left(SCD\right)\right)=\dfrac{2}{3}d\left(H;\left(SCD\right)\right)=\dfrac{2a\sqrt{21}}{21}\)
c.
Từ H kẻ \(HK\perp SA\)
Do \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HK\)
\(\Rightarrow HK\perp\left(SAD\right)\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(HK=\dfrac{SH.AH}{\sqrt{SH^2+AH^2}}=\dfrac{a\sqrt{3}}{4}\)
Do \(BC||AD\Rightarrow BC||\left(SAD\right)\Rightarrow d\left(BC;SD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà \(\left\{{}\begin{matrix}BH\cap\left(SAD\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(BC;SD\right)=d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)=\dfrac{a\sqrt{3}}{2}\)

Ta có
\(SH\perp\left(ABCD\right);SH\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(ABCD\right)\)
Trong mp (ABCD) từ C dựng đường thẳng vuông góc với BD cắt BD tại F ta có
\(SH\perp\left(ABCD\right);CF\in ABCD\Rightarrow SH\perp CF\)
Mà \(CF\perp BD\)
Ta có \(BD\in\left(SBD\right);SH\in\left(SBD\right)\)
\(\Rightarrow CF\perp\left(SBD\right)\) => CF là khoảng cách từ C đến (SBD)
Trong mp (ABCD) nối CH cắt AD tại E
Ta có BC//AD \(\Rightarrow\dfrac{BC}{ED}=\dfrac{HB}{HD}=\dfrac{HC}{HE}=1\Rightarrow ED=BC=\dfrac{3a}{2}\)
\(\Rightarrow EA=AD-ED=3a-\dfrac{3a}{2}=\dfrac{3a}{2}=BC\)
Mà BC//AE và \(\widehat{ABC}=90^o\)
=> ABCE là hình chữ nhật
Trong mp (ABCD) từ H dựng đường thẳng vuông góc với CD cắt CD tại K
Xét tg vuông CDE có
\(CD=\sqrt{CE^2+ED^2}=\sqrt{4a^2+\dfrac{9a^2}{4}}=\dfrac{5a}{2}\)
Xét tg vuông ABD có
\(BD=\sqrt{AB^2+AD^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}\)
\(\Rightarrow HB=HD=\dfrac{BD}{2}=\dfrac{a\sqrt{13}}{2}\)
Xét tg vuông CKH và tg vuông CED có \(\widehat{ECD}\) chung
=> tg CKH đồng dạng với tg CED (g.g.g)
\(\Rightarrow\dfrac{CK}{CE}=\dfrac{HC}{CD}\Rightarrow CK=\dfrac{CE.HC}{CD}=\dfrac{2a.a}{\dfrac{5a}{2}}=\dfrac{4a}{5}\)
Xét tg vuông CKH có
\(HK=\sqrt{HC^2-CK^2}=\sqrt{a^2-\dfrac{16a^2}{25}}=\dfrac{3a}{5}\)
Xét tg vuông DKH và tg vuông DFC có \(\widehat{BDC}\) chung
=> tg DKH đồng dạng với tg DFC (g.g.g)
\(\Rightarrow\dfrac{HK}{CF}=\dfrac{HD}{CD}\Rightarrow CF=\dfrac{HK.CD}{HD}=\dfrac{\dfrac{3a}{5}.\dfrac{5a}{2}}{\dfrac{a\sqrt{13}}{2}}=\dfrac{3a\sqrt{13}}{13}\)