Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ

Tam giác ABC vuông tại A, ta tính được AC:
\(AC^2=BC^2-AB^2=25a^2-9a^2=16a^2\Rightarrow AC-4a\)
Trong mặt phẳng (SAC), qua S kẻ SH vuông góc với AC, H thuộc ACTa có:\(SH=SA.sin30^0=2a\sqrt{3}.\frac{1}{2}=a\sqrt{3}\)\(AH=SA.cos30^0=2a\sqrt{3}.\frac{\sqrt{3}}{2}=3a\)Thể tích khối chóp S.ABC: \(V_{S.ABC}=\frac{1}{2}.SH.S_{\Delta ABC}=\frac{1}{3}.a\sqrt{3}.\frac{1}{2}.3a.4a=2\sqrt{3}a\)Trong mặt phẳng đáy (ABC), qua H kẻ HK vuông góc với BC và cắt BC tại KTam giác HKC đồng dạng với tam giác BAC, ta được:\(\frac{HK}{AB}=\frac{HC}{BC}=\frac{a}{5a}=\frac{1}{5}\rightarrow HK=\frac{1}{5}AB=\frac{1}{5}.3a=\frac{3}{5}a\)Nối SK. Trong mặt phẳng (SHK), từ H kẻ HI vuông góc với SKTa chứng minh được HI vuông góc với mặt phẳng (SBC):Ta có:\(\begin{cases}HK\perp BC\\BC\perp SH\end{cases}\Rightarrow BC\perp\left(SHK\right)\Rightarrow BC\perp HI\)mặt khác: BC_|_HI (1)
HI_|_SK(2)từ (1) (2)=> HI_|_(SBC)Khoảng cách từ điểm H đến mặt phẳng (ABC) là HIXác định khoảng cách từ A đến mặt phẳng (ABC)Suy ra khoảng cách từ A đến mặt phẳng (SBC) được tính theo:

a.
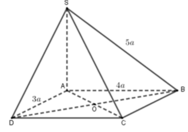
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\) \(\Rightarrow SH\perp CD\)
Gọi E là trung điểm CD \(\Rightarrow HE||BC\Rightarrow HE\perp CD\)
\(\Rightarrow CD\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a), \(HE=BC=a\)
Hệ thức lượng: \(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Do \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=\dfrac{a\sqrt{21}}{7}\)
b.
Theo tính chất trọng tâm, ta có \(GS=\dfrac{2}{3}HS\)
Mà \(HG\cap\left(SCD\right)=S\Rightarrow d\left(G;\left(SCD\right)\right)=\dfrac{2}{3}d\left(H;\left(SCD\right)\right)=\dfrac{2a\sqrt{21}}{21}\)
c.
Từ H kẻ \(HK\perp SA\)
Do \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HK\)
\(\Rightarrow HK\perp\left(SAD\right)\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(HK=\dfrac{SH.AH}{\sqrt{SH^2+AH^2}}=\dfrac{a\sqrt{3}}{4}\)
Do \(BC||AD\Rightarrow BC||\left(SAD\right)\Rightarrow d\left(BC;SD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà \(\left\{{}\begin{matrix}BH\cap\left(SAD\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(BC;SD\right)=d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)=\dfrac{a\sqrt{3}}{2}\)

Ta có
\(SH\perp\left(ABCD\right);SH\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(ABCD\right)\)
Trong mp (ABCD) từ C dựng đường thẳng vuông góc với BD cắt BD tại F ta có
\(SH\perp\left(ABCD\right);CF\in ABCD\Rightarrow SH\perp CF\)
Mà \(CF\perp BD\)
Ta có \(BD\in\left(SBD\right);SH\in\left(SBD\right)\)
\(\Rightarrow CF\perp\left(SBD\right)\) => CF là khoảng cách từ C đến (SBD)
Trong mp (ABCD) nối CH cắt AD tại E
Ta có BC//AD \(\Rightarrow\dfrac{BC}{ED}=\dfrac{HB}{HD}=\dfrac{HC}{HE}=1\Rightarrow ED=BC=\dfrac{3a}{2}\)
\(\Rightarrow EA=AD-ED=3a-\dfrac{3a}{2}=\dfrac{3a}{2}=BC\)
Mà BC//AE và \(\widehat{ABC}=90^o\)
=> ABCE là hình chữ nhật
Trong mp (ABCD) từ H dựng đường thẳng vuông góc với CD cắt CD tại K
Xét tg vuông CDE có
\(CD=\sqrt{CE^2+ED^2}=\sqrt{4a^2+\dfrac{9a^2}{4}}=\dfrac{5a}{2}\)
Xét tg vuông ABD có
\(BD=\sqrt{AB^2+AD^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}\)
\(\Rightarrow HB=HD=\dfrac{BD}{2}=\dfrac{a\sqrt{13}}{2}\)
Xét tg vuông CKH và tg vuông CED có \(\widehat{ECD}\) chung
=> tg CKH đồng dạng với tg CED (g.g.g)
\(\Rightarrow\dfrac{CK}{CE}=\dfrac{HC}{CD}\Rightarrow CK=\dfrac{CE.HC}{CD}=\dfrac{2a.a}{\dfrac{5a}{2}}=\dfrac{4a}{5}\)
Xét tg vuông CKH có
\(HK=\sqrt{HC^2-CK^2}=\sqrt{a^2-\dfrac{16a^2}{25}}=\dfrac{3a}{5}\)
Xét tg vuông DKH và tg vuông DFC có \(\widehat{BDC}\) chung
=> tg DKH đồng dạng với tg DFC (g.g.g)
\(\Rightarrow\dfrac{HK}{CF}=\dfrac{HD}{CD}\Rightarrow CF=\dfrac{HK.CD}{HD}=\dfrac{\dfrac{3a}{5}.\dfrac{5a}{2}}{\dfrac{a\sqrt{13}}{2}}=\dfrac{3a\sqrt{13}}{13}\)
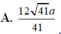
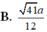
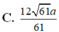
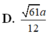

(xin lỗi vì mình không biết chèn hình, các bạn chịu khó tự vẽ. Cảm ơn ạ)
Gọi O là giao điểm 2 đường chéo
I là trung điểm BK
H là trung điểm BE
Xét tam giác(tg) BKD có
I là trung điểm BK
O là trung điểm BD
=>OI là đường trung bình của tgBKD
=> OI // KD
=> OI \(\perp\)BK
Lại có I là trung điểm BK
=> O \(\in\)đường trung trực của BK
*Tương tự ta sẽ chứng minh được O \(\in\)đường trung trực của BE
Từ đó suy ra O là trực tâm của tgBKE
Ta có BO = BD:2
<=> BO = \(\frac{5}{2}\)
Vậy...
Done~
Giao điểm 3 đường trung trực thì liên quan gì tới trực tâm bạn nhỉ?