Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tg vuông AHD và tg vuông AKB có
\(\widehat{BAK}+\widehat{ABC}=90^o\)
\(\widehat{DAH}+\widehat{ADC}=90^o\)
Mà \(\widehat{ABC}=\widehat{ADC}\) (Hai góc đối của hbh)
\(\Rightarrow\widehat{DAH}=\widehat{BAK}\)
=> tg AHD đồng dạng với tg AKB \(\Rightarrow\frac{AH}{AK}=\frac{DA}{AB}\) mà AB = DC (hai cạnh đối của hbh) \(\Rightarrow\frac{AH}{AK}=\frac{DA}{DC}\left(dpcm\right)\)
b/ Ta có K và H đều nhìn AC dưới 1 góc 90 độ
=> Tứ giác AKCH là tứ giác nội tiếp đường tròn đường kính AC
=> sđ \(\widehat{AKH}\) = sđ \(\widehat{ACH}\) = 1/2 sđ cung AH (Góc nội tiếp đường tròn) \(\Rightarrow\widehat{AKH}=\widehat{ACH}\left(dpcm\right)\)

a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông cân tại C

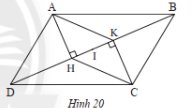
a) Vì \(AH\), \(CK\) vuông góc với \(BD\) (gt)
Suy ra \(AH\) // \(CK\)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Xét \(\Delta ADH\) và \(\Delta CBK\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{CKB}}} = 90^\circ \) (gt)
\(AD = BC\) (cmt)
\(\widehat {{\rm{ADH}}} = \widehat {{\rm{CBK}}}\) (do \(AD\) // \(BC\))
Suy ra \(\Delta ADH = \Delta CBK\) (ch-gn)
Suy ra \(AH = CK\) (hai cạnh tương ứng)
Mà \(AH\) // \(CK\) (cmt)
Suy ra \(AHCK\) là hình bình hành
b) Vì \(AHCK\) là hình bình hành nên hai đường chéo \(HK\) và \(AC\) cắt nhau tại trung điểm.
Mà \(I\) là trung điểm của \(HK\).
Suy ra \(I\) là trung điểm của \(AC\).
Ta lại có \(ABCD\) là hình bình hành nên hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm.
Suy ra \(I\) là trung điểm của \(BD\) hay \( IB = ID\)

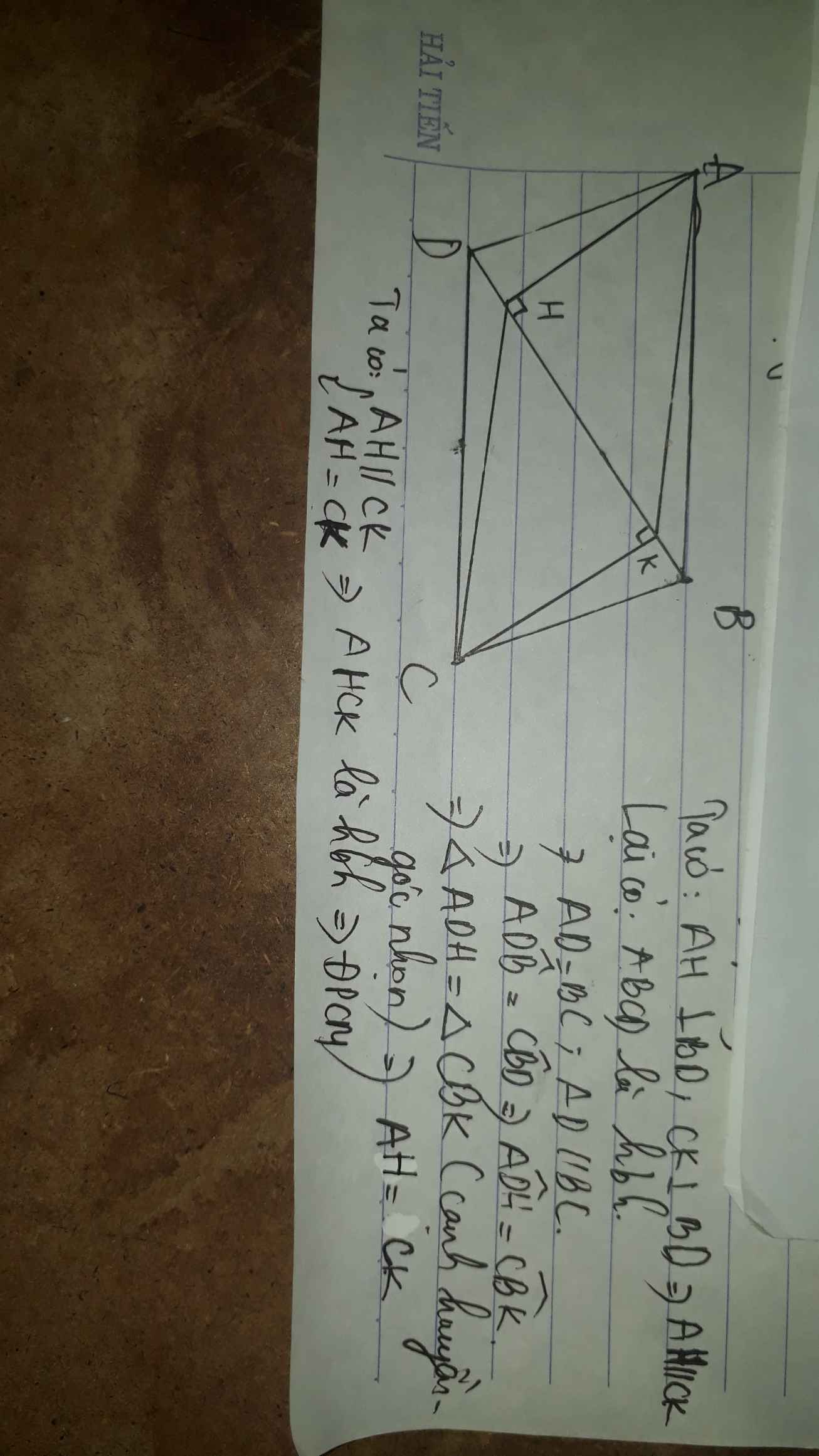
Sửa đề: Từ A,C hạ AH,CK lần lượt vuông góc với BD
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
=>AH=CK
AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành

Xem ở đây nha:
Cho hình bình hành ABCD, Gọi H và K lần lượt là hình chiếu của A và C lên đường chéo BD. a) Chứng minh AHCK là hình bình hành. b) Gọi O là trung điểm của HK. Chứng minh ba điểm A, O, C thẳng hàng - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
Xét tam giác vuông ADH & tam giác vuông CKB:
AD = BC ( ABCD là hbh)
góc D1= góc B1 ( so le trong)
=> tam giác vuông = tam giác vuông CKB ( cạnh hyền - góc nhọn)
=> AH = CK ( 2 cạnh t/ứng)
Xét tứ giác AHCK :
AH = CK (cmt)
AH // CK ( cùng vuông góc vs BD)
=> AHCK là hình bình hành ( đn)

Xét ΔAHD vuông tại H và ΔAKB vuông tại K có
AH=AK
góc HAD=góc KAB
=>ΔAHD=ΔAKB
=>AD=AB
=>ABCD là hình thoi