Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

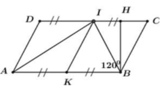
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A

b tham khảo nha
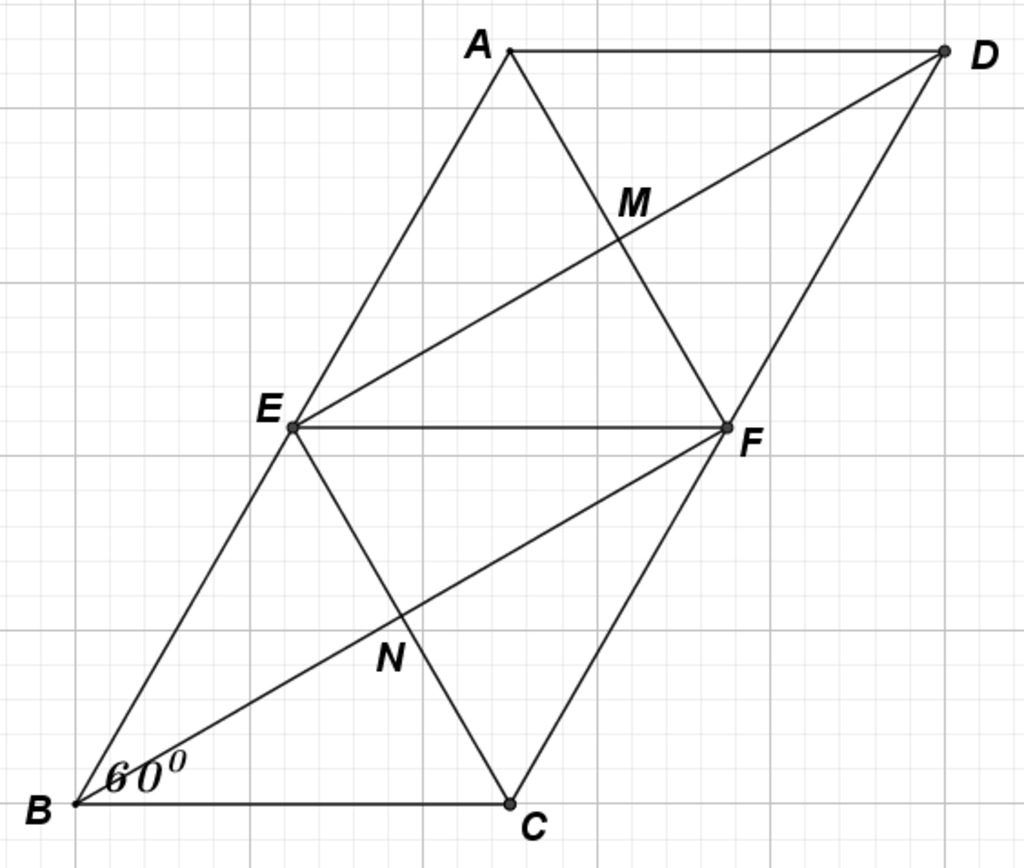
a) Do ABCD là hình bình hành nên AB= CD và AB//CD
Và E và F là trung điểm của AB và CD => AE=BE=CF=DF và BE//DF
Xét tứ giác DEBF có : BE//DF và BE=DF=> DEBF là hình bình hành
b)
Xét AEDF có AE//DF và AE=DF=> AEDF là hình bình hành
Lại có: CD= 2BC= 2 AD nên AD= AE (=1/2 CD)
=> hình bình hành AEDF là hình thoi
c)ta cm được AECF là hình bình hành và M, N là trung điểm của AF và CE
=> MF= EN và MF//EN=> EMFN là hình bình hành
Lại có AEDF là hình thoi nên AN⊥DE tại M
=> góc EMF vuông=> hình bình hành EMFN là hình chữ nhật
d) Chứng minh được
SAFB=12SABCDSBEC=14SABCDˆB=600⇒ΔBECdeucanh=AB2=2(cm)⇒SBEC=√3(cm2)⇒SAFB

a: Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
Xét tứ giác AMND có
AM//ND
AM=ND
AM=AD
=>AMND là hình thoi
b: AMND là hình thoi
=>I là trung điểm chung của AN và MD và AN vuông góc MD tại N
Xét tứ giác MBCN có
MB//CN
MB=CN
MB=BC
=>MBCN là hình thoi
=>MC vuông góc BN tại K và K là trung điểm chung của MC và BN
Xét ΔMDC có
MN là trung tuyến
MN=DC/2
=>ΔMDC vuông tại M
Xét tứ giác MINK có
góc MIN=góc MKN=góc IMK=90 độ
=>MINK là hình chữ nhật
c: Xét ΔMDC có MI/MD=MK/MC
nên IK//DC