Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm của AC, BD
Vì O là tâm đối xứng của hình bình hành nên ta có:
MN đi qua O và OM = ON
hiển nhiên O là trung điểm EF
=> MENF là hình bình hành (1)
mặt khác:
EF = FD = 2OF => OF = FD/2
từ AD = FD = BD/3 và ON là đường trung bình của tgiác ACD nên
ON = AD/2 = FD/2 = OF => MN = EF (2)
từ (1) và (2) => MENF là hình chữ nhật
b) MENF là hình vuông khi và chỉ khi hình chữ nhật MENF có 2 đường chéo vuông góc: MN vuông EF
<=> MN vuông BD <=> AD vuông BD
chúc you học tốt!! ^^
ok mk nha!!! 45464564556765587696532543545654645654645756756756756585634564634
bn đang hok lớp 8 ak giống mk!! ^^
76756768534556345634346654767567636456574675765

a) Xét hình bình hành ABCD, có:
AB = DC (2 cạnh hình bình hành)
mà M là trung điểm AB (gt)
N là trung điểm CD (gt)
=> AM = MB = DN = NC
Xét tam giác BEM và tam giác DFN, có:
DF = BE (gt)
góc MBE = góc FDN (so le trong của AB // DC)
DN = MB (cmt)
=> tam giác BEM = tam giác DFN (c-g-c) (đpcm)
=> góc BEM = góc DFN (2 góc tương ứng)
=> ME = FN (2 cạnh tương ứng)
mà góc BEM + góc MED = 180 độ
góc DFN + góc NFE = 180 độ
=> góc MED = góc NFE
mà 2 góc nằm ở vị trí so le trong của ME và FN
=> ME // FN
Xét tứ giác MENF, có:
ME = FN (cmt)
mà ME // FN (cmt)
=> tứ giác MENF là hình bình hành (đpcm)
b) Ta có: BD = 3AD (gt)
mà BD = DF + FE + EB (DF = FE = EB - gt)
=> BD = 3DF = 3FE = 3EB
=> DF = FE = EB = AD
Xét tứ giác AMDN, có:
AM // DN (AB // CD; M thuộc AB; N thuộc CD)
AM = DN (cmt)
=> tứ giác AMDN là hình bình hành
=> AD = MN (2 cạnh bên bằng nhau)
Xét tứ giác MENF, có:
MN = AD (cmt)
FE = AD (cmt)
=> MN = FE
mà MN và FE là 2 đường chéo tứ giác MENF
=> MENF là hình chữ nhật (vì hình chữ nhật có 2 đường chéo bằng nhau) (đpcm)

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

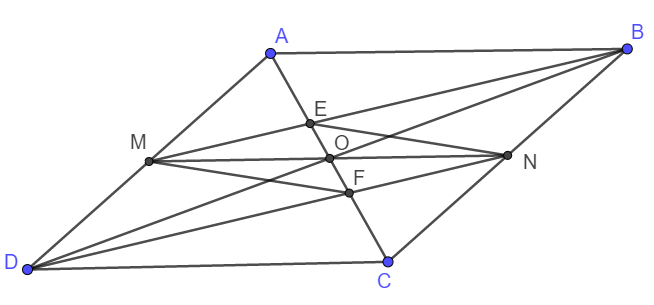
a) Do ABCD là hình bình hành nên AD song song và bằng BC.
Lại có M, N là trung điểm AD, BC nên DM song song và bằng BN. Suy ra DMBN là hình bình hành, hay MB//DN.
Xét tam giác ADF, có:
M là trung điểm AC
ME//DF
\(\Rightarrow\) ME là đường trung bình tam giác ADF.
Vậy AE = EF.
Hoàn toàn tương tự : EF = FC.
Vậy nên AE = EF = FC.
b) DMBN là hình bình hành nên hai đường chéo DB và MN cắt nhau tại trung điểm mỗi đường.
Vậy thì O là trung điểm MN.
Lại có: AO = OC; AE = FC nên AO - AE = OC - FC hay EO = OF.
Xét tứ giác MENF có O là trung điểm hai đường chéo EF và MN nên MENF là hình bình hành.
c)
+) Để hình bình hành MENF là hình chữ nhật thì hai đường chéo MN và EF bằng nhau.
Lại có MN = AB, EF = \(\frac{AC}{3}\). Vậy hình bình hành ABCD phải có đường chéo AC = 2AB thì MENF là hình chữ nhật.
+) Để hình bình hành MENF là hình thoi thì hai đường chéo MN và EF phải vuông góc.
Vậy thì \(EF\perp MN\Rightarrow AC\perp AB\)
Vậy hình bình hành ABCD phải có đường chéo AC vuông góc với cạnh AB thì MENF là hình thoi.
+) Để hình bình hành MENF là hình vuông thì nó vừa là hình chữ nhật, vừa là hình thoi.
Vậy thì hình bình hành ABCD có đường chéo AC vuông góc với AB và AC = 2AB.