Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADN và ΔCBM có
góc A=góc C
AD=CB
góc ADN=góc CBM
=>ΔADN=ΔCBM
b: ΔADN=ΔCBM
=>AN=CM
AN+NB=AB
CM+MD=CD
mà AN=CM và AB=CD
nên NB=MD
mà NB//MD
nên NBMD là hình bình hành
c: Xét tứ giác AMCN có
AN//CM
AN=CM
=>AMCN là hình bình hành

a, Vì AD//BC (hbh ABCD) nên \(\widehat{AIB}=\widehat{IAD}\left(so.le.trong\right)\)
Mà \(\widehat{BAI}=\widehat{IAD}\) (AI là p/g) nên \(\widehat{BAI}=\widehat{AIB}\)
Do đó tg ABI cân tại B
a: Xét ΔBAI có \(\widehat{BAI}=\widehat{BIA}\)
nên ΔBAI cân tại B

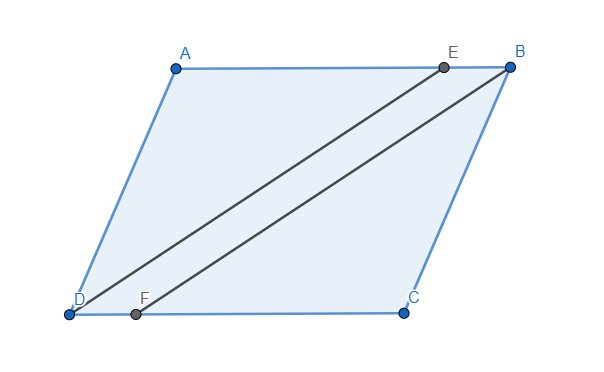
a) Ta thấy \(\widehat{AED}=\widehat{EDC}=\widehat{ADE}\) nên tam giác ADE cân tại A. Hoàn toàn tương tự thì tam giác CBF cân tại C.
Mặt khác, do tứ giác ABCD là hình bình hành nên \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\). Do đó \(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{D}}{2}\) hay \(\widehat{CBF}=\widehat{ADE}\). Kết hợp với \(\widehat{A}=\widehat{C}\) thì suy ra \(\Delta ADE~\Delta CBF\left(g.g\right)\). Lại có \(\dfrac{AD}{CB}=1\) (do tứ giác ABCD là hình bình hành), suy ra \(\Delta ADE=\Delta CBF\) (2 tam giác đồng dạng có tỉ số đồng dạng bằng 1 thì 2 tam giác đó bằng nhau), ta có đpcm.
b) Ta thấy \(\widehat{AED}=\widehat{ADE}=\widehat{CBF}=\widehat{ABF}\) nên DE//BF. Lại có BE//DF (do tứ giác ABCD là hình bình hành) nên tứ giác DEBF cũng là hình bình hành (các cặp cạnh đối song song).
a/
Xét tg ADE có
\(\widehat{ADE}=\widehat{CDE}\) (gt) (1)
\(\widehat{AED}=\widehat{CDE}\) (góc so le trong) (1)
Từ (1) và (2) => \(\widehat{ADE}=\widehat{AED}\) => tg ADE là tg cân tại A
=> AD=AE (3)
Xét tg CBF có
\(\widehat{CBF}=\widehat{ABF}\) (gt) (4)
\(\widehat{CFB}=\widehat{ABF}\) (góc so le trong) (5)
Từ (4) và (5) => \(\widehat{CBF}=\widehat{CFB}\) => tg CBF cân tại C
=> CB=CF (6)
Ta có
AD=CB (cạnh đối hình bình hành) (7)
Từ (3) (6) (7) => AD=AE=CB=CF
Mà \(\widehat{DAE}=\widehat{BCF}\) (góc đối hình bình hành)
=> tg ADE = tg CBF (c.g.c)
=> tg ADE và tg CBF là những tg cân bằng nhau
b/
tg ADE = tg CBF (cmt) \(\Rightarrow\widehat{BFC}=\widehat{ADE}\)
Mà \(\widehat{EDC}=\widehat{ADE}\) (gt)
\(\Rightarrow\widehat{BFC}=\widehat{EDC}\) Hai góc này ở vị trí đồng vị => DE//BF (8)
Ta có
AB//CD (cạnh đối hình bình hành) => BE//DF (9)
Từ (8) (9) => DEBF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hình bình hành)

a)Ta có : \(\widehat{A_1}+\widehat{M_1}=90^o;\widehat{M_1}+\widehat{BMC}=90^o\)\(\Rightarrow\widehat{A_1}=\widehat{BMC}\)
Xét \(\Delta ADM\)và \(\Delta BMC\)có : \(\widehat{A_1}=\widehat{BMC}\); \(\widehat{ADM}=\widehat{BCM}\)
\(\Rightarrow\Delta DAM\approx\Delta CMB\left(g.g\right)\)\(\Rightarrow\frac{AD}{DM}=\frac{CM}{BC}\)hay CM = \(\frac{5}{2}.5=12,5\)
b) \(\Delta AMB\)có EK là tia phân giác nên \(\frac{EA}{EB}=\frac{MA}{MB}\)( 1 )
Mặt khác : \(\widehat{B_1}+\widehat{EKB}=90^o;\widehat{B_1}+\widehat{A_2}=90^o\)nên \(\widehat{A_2}=\widehat{EKB}\)
\(\Delta BEK\approx\Delta BMA\left(g.g\right)\)\(\Rightarrow\frac{EK}{EB}=\frac{MA}{MB}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra EA = EK
c) Ta có : \(\widehat{BMH}=90^o\)nên \(BM\perp AH\)
Xét \(\Delta AHB\)có \(BM\perp AH\); \(HE\perp AB\)nên K là trực tâm \(\Rightarrow AN\perp BH\)
\(\Rightarrow\widehat{ANH}=90^o\)
xét \(\Delta AHN\)và \(\Delta BMH\)có : \(\widehat{ANH}=\widehat{BMH}=90^o;\widehat{MHN}\left(chung\right)\)
\(\Rightarrow\)\(\Delta AHN\approx\Delta BHM\left(g.g\right)\)\(\Rightarrow\)\(\frac{MH}{BH}=\frac{HN}{AH}\)hay \(\frac{MH}{HN}=\frac{BH}{AH}\)
Xét \(\Delta MHN\)và \(\Delta AHB\)có : \(\widehat{MHN}\left(chung\right);\frac{MH}{HN}=\frac{BH}{AH}\)
\(\Rightarrow\)\(\Delta HMN\approx\Delta HBA\left(g.g\right)\) \(\Rightarrow\)\(\widehat{HMN}=\widehat{HBA}\)
Mà EA = EK nên \(\widehat{A_2}=45^o\) \(\Rightarrow\widehat{ABH}=90^o-\widehat{A_2}=45^o\)hay \(\widehat{HMN}=45^o\)
Ta có : \(\widehat{EMN}=180^o-\widehat{AME}-\widehat{HMN}=180^o-45^o-45^o=90^o\)
\(\Rightarrow EM\perp MN\)
Mặt khác : ME là tia phân giác \(\widehat{AMB}\) nên MN là tia phân giác \(\widehat{BMH}\)