Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Nếu HB = HC ⇒ HB2 = HC2.
⇒ AH2 + HB2 = AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 = AC2
⇒ AB = AC
- Nếu AB = AC ⇒ AB2 = AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 = AH2 + HC2
⇒ HB2 = HC2
⇒ HB = HC

AB > AC ⇒ AB2 > AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 > AH2 + HC2
⇒ HB2 > HC2
⇒ HB > HC

A B C D H E I
Lấy E đối xứng với D qua AB, ED cắt AB tại I
Vì AD là phân giác \(\widehat{BAC}\)\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}< 1\)
\(\Rightarrow BD< CD\)
\(\Rightarrow BC>2BD\)
Vì DI // CH
\(\Rightarrow\frac{DI}{CH}=\frac{BD}{BC}< \frac{1}{2}\)
\(\Rightarrow CH>2DI=DE\left(1\right)\)
Xét \(\Delta ABC\)ta có: \(AB< AC< BC\)
\(\Rightarrow\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
\(\Rightarrow2\widehat{BAC}>\widehat{ACB}+\widehat{ABC}\)
\(\Rightarrow\widehat{BAC}>\frac{\widehat{ACB}+\widehat{ABC}}{2}=\frac{180^o-\widehat{BAC}}{2}\)
Xét \(\Delta AED\)ta có:
\(\widehat{AED}=\widehat{ADE}=\frac{180^o-\widehat{EAD}}{2}=\frac{180^o-\widehat{BAC}}{2}< \widehat{BAC}=\widehat{EAD}\)
\(\Rightarrow ED>AE=AD\left(2\right)\)
Từ (1) và (2) \(\Rightarrow CH>AD\)
mk mới học lớp 5 nên ko biết, mong bạn thông cảm, chúc bạn học giỏi nha

A B C H E D
a) tg AHB và tg AHC: AHB^ = AHC^ = 90o; AB = AC; AH chung
=> tg AHB = tg AHC (ch_cgv)
=> HB = HC (2 cạnh t/ứng) ; BAH^ = CAH^ (2 góc t/ứng)
b) BC= BH + HC = 2HC = 8 => HC = BC/2 = 4 (cm)
tg AHC: \(AH=\sqrt{AC^2-HC^2}=\sqrt{25-16}=3\left(cm\right)\)
c) tg ADH và tg AEH: ADH^ = AEH^ = 90o; AH chung; ADH^ = EAH^
=> tg ADH = tg AEH (ch_gn)
=> AD =AE (2 cạnh t/ứng)
Vậy tg DAE cân tại A (AD = AE)

Tự vẽ hình
a, Áp dụng định lý pytago vào tam giác ABH vuông tại H và AcH vuông tại H ta có:
\(BH^2+AH^2=AB^2\Rightarrow BH^2=AB^2-AH^2\left(1\right)\)
\(\text{C}H^2+AH^2=A\text{C}^2\Rightarrow\text{C}H^2=A\text{C}^2-AH^2\left(2\right)\)
Mà AB > AC (3)
Từ (1),(2),(3) => BH > CH
b, Làm tương tự Câu a

Bài này không chứng minh được theo kiến thức lớp 6, 7 và tiểu học. Phải áp dụng tam giác đồng dạng của lớp 8.
Hoàng Tuấn Đăng A hai à, thầy em bảo làm theo cách tiểu học, cách tính S tam giác + lớp 6,7 đó a ạ

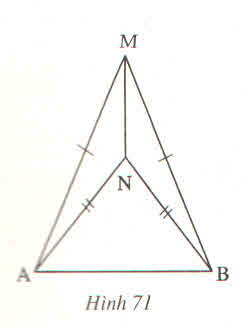
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg
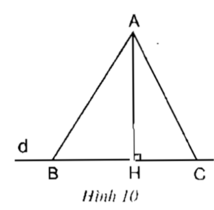
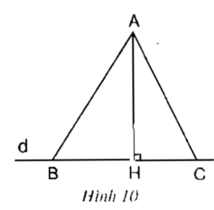
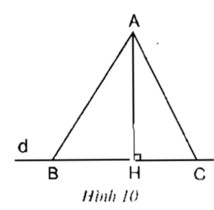
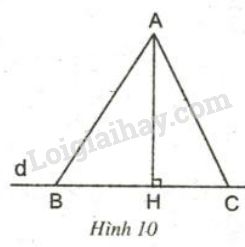
Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2 + HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC2
⇒ AB > AC