Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
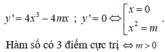
Khi đó đồ thị hàm số có 3 điểm cực trị là:
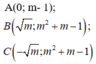
Vì B, C đối xứng với nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác:
![]()
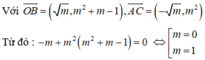
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm

Chọn D
y ' = 4 x 3 - 4 m x
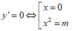
Hàm số có 3 điểm cực trị ⇔ m > 0
Khi đó đồ thị hàm số có 3 điểm cực trị là
A (0;m-1)
B ( m ; m 2 + m - 1 )
C ( - m ; m 2 + m - 1 )
Vì B,C đối xứng nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác ABC
![]()
Với O B ⇀ = ( m , m 2 + m - 1 ) , A C ⇀ = ( - m , m 2 )
![]()
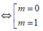
Vậy m = 1 là gtct

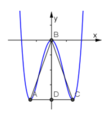
+ Điều kiện để hàm số có 3 cực trị là m> 0
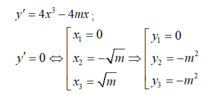
+ Các điểm cực trị tạo thành tam giác cân có đáy bằng 2√m, đường cao bằng m2. (như hình bên )
Ta được S ∆ A B C = 1 2 A C . B D = m . m 2 .
+ Để tam giác có diện tích nhỏ hơn 1 thì m . m 2 < 1 h a y 0 < m < 1
Chọn D.

Chọn B
[Phương pháp tự luận]
Hàm số có 3 điểm cực trị khi m > 0
Ba điểm cực trị là:
![]()
Tứ giác OBAC đã có OB=OC ,AB=AC.
Vậy tứ giác OBAC là hình thoi chỉ cần thêm điều kiện
![]()
![]()
![]()
![]()
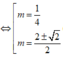 ( thỏa mãn).
( thỏa mãn).

Chọn D
T a c ó y ' = 3 x 2 - 6 ( m + 1 ) x + 12 m
Hàm số có hai cực trị ⇔ y ' = 0 có hai nghiệm phân biệt
![]()
A ( 2 ; 9 m ) , B ( 2 m - 4 m 3 + 12 m 2 - 3 m + 4 )
ABC nhận O làm trọng tâm
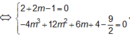
![]()

Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có điểm cực trị khi và chỉ khi y’ = 0 có nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)
Khi đó, ta có:
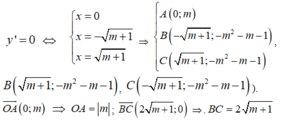
Do đó O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).
Vậy m = 2 ± 2 2 .
Chọn A.

Chọn A
Ta có:
![]()
Hàm số có 3 điểm cực trị khi và chỉ khi :
y ' có 3 nghiệm phân biệt
⇔ m + 1 > 0 ⇔ m > - 1 ( * )
Khi đó, ta có y ' = 0
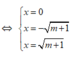
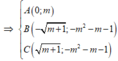
(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử
![]()
Ta có: O A ( 0 ; m ) ⇒ O A = m ⇒ B C = 2 m + 1
Do đó OA = BC
![]()
![]()
⇔ m = 2 ± 2 2 ( t h ỏ a m ã n ) ( * )
Vậy m = 2 ± 2 2

+ Đạo hàm y’ = -4 x3+ 4mx= -4x( x2- m)
Để hàm số có 3 điểm cực trị khi m> 0
+ Tọa độ ba điểm cực trị là: A( 0; 1-4m) ; B ( - m ; m 2 - 4 m + 1 ) ; C ( m ; m 2 - 4 m + 1 )
Tứ giác OBAC đã có OB= OC; AB= AC.
Vậy tứ giác OBAC là hình thoi khi và chỉ khi :
O A = A C h a y ⇔ m + ( m 2 - 4 m + 1 ) 2 = m + m 4 ⇔ ( m 2 - 4 m + 1 ) 2 = m 4

Tổng các giá trị của m thỏa mãn đầu bài là 9/4.
Chọn D.

Ta có đạo hàm y’ = 3x2- 6( m+ 1) x+ 12m.
Hàm số có hai cực trị khi và chỉ khi y’ = 0 có hai nghiệm phân biệt
Hay (m-1) 2> 0 suy ra m≠1 ( *)
Khi đó hai điểm cực trị là A( 2; 9m) : B( 2m; -4m3+ 12m2-3m+ 4).
Tam giác ABC nhận O làm trọng tâm
⇔ 2 + 2 m - 1 = 0 - 4 m 3 + 12 m 2 + 6 m + 4 - 9 2 = 0 ⇔ m = - 1 2 t h ỏ a ( * ) .
Chọn A.
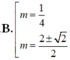
+ Đạo hàm y’ = 4x3- 4mx
Hàm số có 3 điểm cực trị khi và chỉ khi m≠0.
+ Khi đó đồ thị hàm số có 3 điểm cực trị là:
+ Vì B,C đối xứng nhau qua trục tung nên BC và OA vuông góc với nhau.
Do đó O là trực tâm tam giác ABC khi và chỉ khi OB vuông góc AC hay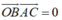
Với
Kết hợp với điều kiện m ≠ 0 thì m = 1 là giá trị cần tìm.
Chọn B.