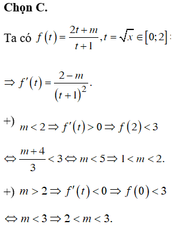Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Em có tập xác định D = ℝ và y ' = − x 2 + 2 m − 1 x + m + 3 .
Yêu cầu bài toán <=> y' = 0 có hai nghiệm phân biệt x 1 , x 2 thỏa mãn x 1 − x 2 ≤ 2 6
y' = 0 có 2 nghiệm phân biệt ⇔ Δ ' = m − 1 2 + m + 3 > 0 ⇔ m 2 − m + 4 > 0 , ∀ m
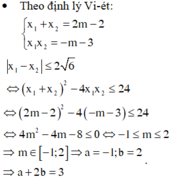

Ta có f ' x = - m 2 + m + 1 x + 1 2 > 0
Suy ra f(x) là hàm đồng biến trên [0;1]
Do đó f 0 ≤ f x ≤ f 1 hay
- m 2 + m ≤ f x ≤ 1 2 - m 2 + m + 1
Khi đó
m i n x ∈ 0 ; 1 f x = - m 2 + m = - 2 ⇔ m = - 1 m = 2
Đáp án A

Đáp án A
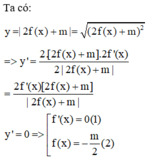
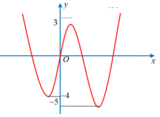
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy