Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Ta có y ' = 3 x 2 - 11 . Giả sử M m ; m 3 - 11 m thì tiếp tuyến ∆ của (C) tại điểm M có hệ số góc là k = y ' m = 3 m 2 - 11
Phương trình ∆ : y = 3 m 2 - 11 x - 2 m .
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng ∆ là:
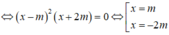
Suy ra hoành độ các điểm Mn lập thành một cấp số nhân (xn) có số hạng đầu x 1 = - 2 và công bội q = -2.
Ta có x n = x 1 . q n - 1 = - 2 n
![]() .
.
Để 11 x n + y n + 2 2019 = 0
⇔ 3 n = 2019 ⇔ n = 673

Đáp án A
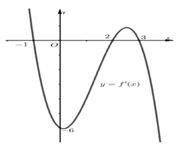
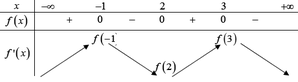
Gọi M x 0 ; y 0 ∈ C ⇒ y ' x 0 = 3 x 0 2 - 3 và y x 0 = x 0 3 - 3 x 0 .
Suy ra phương trình tiếp tuyến của (C) tại M là y = y x 0 = y ' x 0 . x - x 0 .
⇔ y = 3 x 0 2 - 3 . x - x 0 + x 0 3 - 3 x 0 = 3 x 0 2 - 3 . x - 2 x 0 3 ( d ) .
Phương trình hoành độ giao điểm của (C) và (d) là x 3 - 3 x = 3 x 0 2 - 3 x - 2 x 0 3
⇔ x 3 - 3 x 0 2 . x + 2 x 0 3 = 0 ⇔ x - x 0 2 x + 2 x 0 = 0 ⇔ [ x = x 0 x = - 2 x 0 .
Vậy x M = x 0 x N = - 2 x 0 ⇒ 2 x M + x N = 0 .

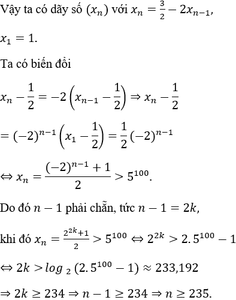
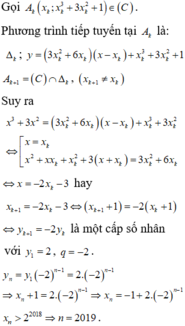

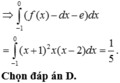
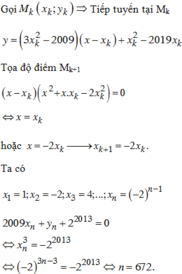
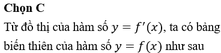


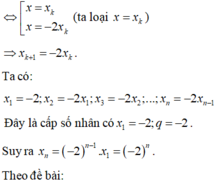

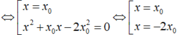
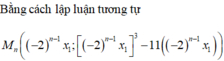
Đáp án đúng : A