Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhìn câu vẽ đồ thị kia là tiêu rồi bạn
Bạn tự vẽ đồ thị, mấy câu sau mình làm thì được

\(y=\frac{1}{3}x^3-\left(m-2\right)x^2+\left(4m-8\right)x+m+1\)
\(y'=f\left(x\right)=x^2-2\left(m-2\right)x+4\left(m-2\right)\) (1)
Để (1) có 2 nghiệm thỏa mãn \(x_1< -2< x_2\) thì:
\(1.f\left(-2\right)< 0\Leftrightarrow4+4\left(m-2\right)+4\left(m-2\right)< 0\)
\(\Leftrightarrow8m< 12\Rightarrow m< \frac{3}{2}\)

Chọn C.
+) Ta có ![]()
![]()
+) Theo giả thiết hàm số đạt cực trị tại ⇔ phương trình (1) có 2 nghiệm phân biệt
![]()
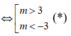
+) Với điều kiện (*) thì phương trình (1) có nghiệm x 1 , x 2 , theo Vi-ét ta có:
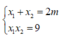
+) Ta lại có ![]()
![]()
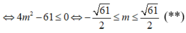
+) Kết hợp (*), (**) và điều kiện m dương ta được: 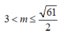


https://diendan.hocmai.vn/threads/can-giai-gap-tim-m-de-hs-co-ctri-tai-x1-x2-sao-cho-x1-2x2-1.247639/

Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

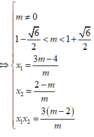

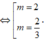
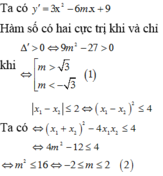

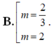
Đáp án A
ta có
Khi đó T = x13 + x23 = -50