Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
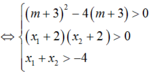
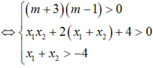
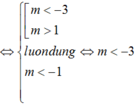
Chọn C

Chọn A
![]()
Hàm số có 2 cực trị ⇔ y ' = 0 có hai nghiệm phân biệt x 1 , x 2 thỏa mãn: - 1 < x 1 < x 2
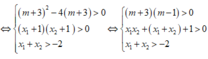
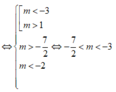

Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

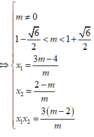

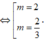

Chọn C
Ta có: y ' = 2 x 2 - 2 m x - 2 ( 3 m 2 - 1 )
g ( x ) = x 2 - m x - 3 m 2 + 1 là tam thức bậc hai có ∆ = 13 m 2 - 4
Do đó hàm số có hai điểm cực trị khi và chỉ khi y ' có hai nghiệm phân biệt
⇔ g ( x ) có hai nghiệm phân biệt

x 1 ; x 2 là các nghiệm của g(x) nên theo định lý Vi-ét, ta có
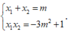

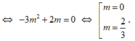
Đối chiếu với điều kiện (1), ta thấy chỉ m = 2 3 thỏa mãn yêu cầu bài toán

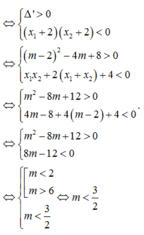

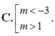
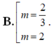





\(y=\frac{1}{3}x^3-\left(m-2\right)x^2+\left(4m-8\right)x+m+1\)
\(y'=f\left(x\right)=x^2-2\left(m-2\right)x+4\left(m-2\right)\) (1)
Để (1) có 2 nghiệm thỏa mãn \(x_1< -2< x_2\) thì:
\(1.f\left(-2\right)< 0\Leftrightarrow4+4\left(m-2\right)+4\left(m-2\right)< 0\)
\(\Leftrightarrow8m< 12\Rightarrow m< \frac{3}{2}\)