Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
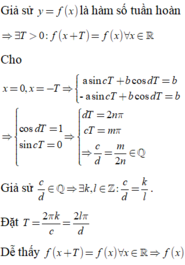
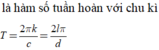
· Bổ trợ kiến thức: Thường thì ở những bài toán như trên các em có thể suy luận được ngay c d mới có sự liên quan và quyết định đến việc hàm số y = f(x)có tuần hoàn hay không.
Tuy nhiên chỉ cần nhận ra được chiều thuận “y= f(x)=asincx+bcosdx là hàm số tuần hoàn => c d là số hữu tỉ” là các em đã thấy ngay được phương án đúng rồi, để chứng minh chiều ngược lại thì đó là điều không dễ dàng.
Các em ghi nhớ luôn nhé – để áp dụng vào các bài tập khác: “Cho a,b,c,d là các số thực khác 0 và hàm số y= f(x)=asincx+bcosdx, khi đó y= f(x)=asincx+bcosdxlà hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ”

Thịnh ơi, có gì mấy câu trả lời SGK em giúp anh trình bày đầy đủ và làm đẹp nhé, có Latex đầy đủ á. Mình làm hướng đến cộng đồng, em giúp hoc24 nhé!
a) Ta có: \(\Delta x = x - {x_0},\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\)
\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{h({x_0} + \Delta x) - h({x_0})}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{h\left( x \right) - h\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x) + g(x) - f({x_0}) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{g(x) - f\left( {{x_0}} \right)}}{{x - {x_0}}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{g\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {{x_0} + \Delta x} \right) - g\left( {{x_0}} \right)}}{{\Delta x}}\end{array}\)
b) \(h'({x_0})\) = \(f'({x_0}) + g'({x_0})\)

Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) - f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.

1. Áp dụng quy tắc L'Hopital
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)
2.
\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)
2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm
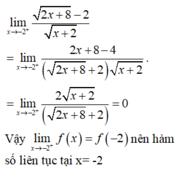
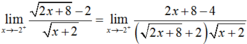
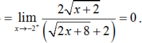
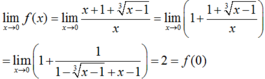
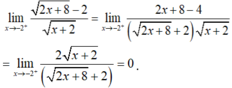
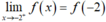 nên hàm số liên tục tại x = -2
nên hàm số liên tục tại x = -2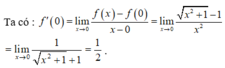
Chọn D.
Ta có: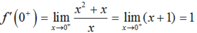
và