LV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2023
Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
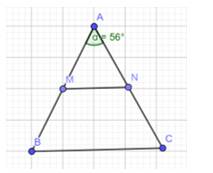
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
a)
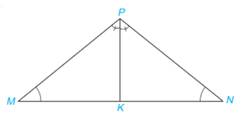
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
5 tháng 1 2018
Câu 1 : C
Câu 2 : C
Câu 3 :
a) Xét tam giác AMB và tam giác DMC , có :
AM = DM ( gt )
BM = CM ( gt )
góc AMB = góc DMC ( đối đỉnh )
=> tam giác AMB = tam giác DMC
=> DC = AB ( hai cạnh tương ứng )
Vậy DC = AB
b) Xét tam giác AKM và tam giác DHM , có :
góc AKM = góc DHM ( = 90o )
góc M1 = góc M2 ( đối đỉnh )
MA = MD ( gt )
=> tam giác AKM = tam giác DHM ( g-c-g )
=> HD = AK ( hai cạnh tương ứng )
=> góc KAM = góc HDM ( hai góc tương ứng ) mà hai góc ở vị trí so le trong nên HD // AK ( dấu hiệu nhận biết hai đường thẳng song song )
Vậy HD = AK ; HD // AK ( đpcm )
11 tháng 6 2022
a: Xét ΔCAM có CA=CM
nên ΔCAM cân tại C
=>\(\widehat{CAM}=\widehat{CMA}\)
b: \(\widehat{CAM}+\widehat{MAN}=90^0\)
=>\(\widehat{CMA}+\widehat{MAN}=90^0\)
c: \(\widehat{BAM}+\widehat{CAM}=90^0\)
\(\widehat{CMA}+\widehat{HAM}=90^0\)
DO đó: \(\widehat{BAM}=\widehat{HAM}\)
hay AM là tia phân giác của góc BAH
d: Xét ΔHAM và ΔNAM có
AH=AN
\(\widehat{HAM}=\widehat{NAM}\)
AM chung
DO đó: ΔHAM=ΔNAM
Suy ra: \(\widehat{AHM}=\widehat{ANM}=90^0\)
=>MN\(\perp\)AB
VM
4 tháng 12 2019
a) Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)
=> \(\left\{{}\begin{matrix}AB=AC\\\widehat{B}=\widehat{C}\end{matrix}\right.\) (tính chất tam giác cân).
Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(\widehat{B}+\widehat{C}=180^0-\widehat{A}\) (1).
Mà \(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\widehat{B}=\widehat{C}=\frac{\widehat{A}}{2}\) (2).
Từ (1) và (2) => \(\widehat{B}=\widehat{C}=180^0-\frac{\widehat{A}}{2}.\)
b) Xét 2 \(\Delta\) vuông \(AHB\) và \(AHC\) có:
\(\widehat{AHB}=\widehat{AHC}=90^0\left(gt\right)\)
\(AB=AC\left(cmt\right)\)
Cạnh AH chung
=> \(\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông).
=> \(HB=HC\) (2 cạnh tương ứng).
=> \(\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng).
c) Ta có:
\(\left\{{}\begin{matrix}AM+BM=AB\\AN+CN=AC\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}BM=CN\left(gt\right)\\AB=AC\left(cmt\right)\end{matrix}\right.\)
=> \(AM=AN.\)
=> \(\Delta AMN\) cân tại A.
Chúc bạn học tốt!
mn 7cm nha