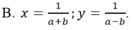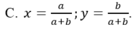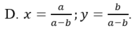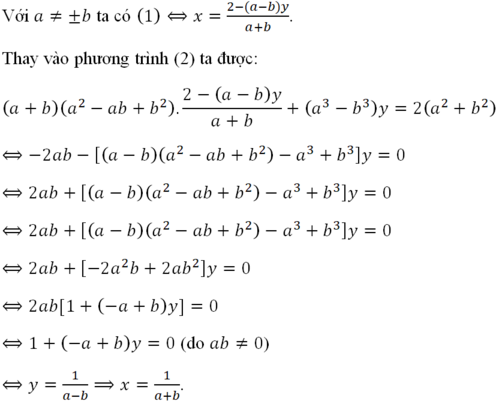CD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
2
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
1. Ta sẽ chứng minh dựa trên các kết quả quen thuộc sau về tâm I của đường tròn nội tiếp tam giác:
\(a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\overrightarrow{0}\)
Và: \(a.IA^2+b.IB^2+c.IC^2=abc\)
Đẳng thức thứ nhất chỉ cần dựng hình bình hành AMIN, sau đó sử dụng định lý phân giác các góc B và C.
Đẳng thức thứ hai ta chỉ cần lấy 1 điểm P nào đó đối xứng I qua AC, gọi D, E, F là tiếp điểm của (I) với BC, AC, AB, sau đó sử dụng tỉ lệ diện tích:
\(\dfrac{S_{AEIF}}{S_{ABC}}=\dfrac{S_{AIK}}{S_{ABC}}=\dfrac{AI.AK}{AB.AC}=\dfrac{IA^2}{bc}\)
Tương tự và cộng lại ...
Từ đó:
\(a.MA^2+b.MB^2+c.MC^2=a.\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+b\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+c.\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2\)
\(=\left(a+b+c\right)MI^2+a.IA^2+b.IB^2+c.IC^2+2\overrightarrow{MI}\left(a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}\right)\)
\(=\left(a+b+c\right)MI^2+abc\ge abc\)
Dấu "=" xảy ra khi \(MI=0\) hay M là tâm đường tròn nội tiếp
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
2. Do a;b;c là độ dài 3 cạnh của tam giác, thực hiện phép thế Ravi:
Đặt \(\left(a;b;c\right)=\left(x+y;y+z;z+x\right)\)
BĐT cần chứng minh tương đương:
\(4\left(x+y+z\right)\left(x^2+y^2+z^2+xy+yz+zx\right)\ge3\left(x^3+y^3+z^3+3xyz+xy\left(x+y\right)+yz\left(y+z\right)+zx\left(z+x\right)\right)\)
\(\Leftrightarrow x^3+y^3+z^3+3xyz\ge xy\left(x+y\right)+yz\left(y+z\right)+zx\left(z+x\right)\)
Đây là BĐT Schur bậc 3
CM
15 tháng 3 2018
A sai khi c ≤ 0; B sai, chẳng hạn khi a < 0 < b; C sai chẳng hạn khi a < b < 0.
Đáp án: D
M
0
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2021
\(\left(a^3+b^3\right)\left(a+b\right)=ab\left(1-a\right)\left(1-b\right)\)
\(\Leftrightarrow\left(1-a\right)\left(1-b\right)=\left(\dfrac{a^2}{b}+\dfrac{b^2}{a}\right)\left(a+b\right)\ge\left(a+b\right)^2\ge4ab\)
\(\Rightarrow1+ab-4ab\ge a+b\ge2\sqrt{ab}\)
\(\Rightarrow3ab+2\sqrt{ab}-1\le0\)
\(\Leftrightarrow\left(\sqrt{ab}+1\right)\left(3\sqrt{ab}-1\right)\le0\)
\(\Leftrightarrow ab\le\dfrac{1}{9}\)
AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Bài 1:
Áp dụng BĐT Bunhiacopxky ta có:
$(a^2+b^2+c^2)(1+1+1)\geq (a+b+c)^2$
$\Leftrightarrow 3(a^2+b^2+c^2)\geq 1$
$\Leftrightarrow a^2+b^2+c^2\geq \frac{1}{3}$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$
AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Bài 2:
Áp dụng BĐT Bunhiacopxky:
$(a^2+4b^2+9c^2)(1+\frac{1}{4}+\frac{1}{9})\geq (a+b+c)^2$
$\Leftrightarrow 2015.\frac{49}{36}\geq (a+b+c)^2$
$\Leftrightarrow \frac{98735}{36}\geq (a+b+c)^2$
$\Rightarrow a+b+c\leq \frac{7\sqrt{2015}}{6}$ chứ không phải $\frac{\sqrt{14}}{6}$ :''>>