Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy

Chọn C
* Số tam giác có 2 đỉnh thuộc
d
1
và 1 đỉnh thuộc
d
2
là: ![]() .
.
* Số tam giác có 1 đỉnh thuộc
d
1
và 2 đỉnh thuộc
d
2
là: ![]() .
.
Vậy có 70 + 105 = 175 tam giác.

Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có ![]() tam giác.
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có ![]() tam giác.
tam giác.
Theo bài ra ta có: ![]()
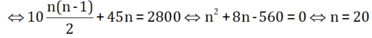
Chọn A.

Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d 1 và hai đỉnh thuộc d 2 .
Loại này có C 10 1 . C n 2 tam giác.
Loại 2: Tam giác có một đỉnh thuộc d 2 và hai đỉnh thuộc d 1 .
Loại này có C 10 2 . C n 1 tam giác.
Theo bài ra ta có: C 10 1 . C n 2 + C 10 2 . C n 1 = 2800
⇔ 10 n ( n − 1 ) 2 + 45 n = 2800 ⇔ n 2 + 8 n − 560 = 0 ⇔ n = 20
Chọn đáp án D

Xét 2 trường hợp:
Th1: 1 điểm trên d1, 2 điểm trên d2
Chọn 1 điểm trên d1 có \(C_{17}^1\) (cách)
Chọn 2 điểm trên d2 có \(C^2_{20}\) (cách)
\(\Rightarrow C^1_{17}.C^2_{20}\) (tam giác)
Th2: 1 điểm trên d2, 2 điểm trên d1
Chọn 1 điểm trên d2 \(C^1_{20}\left(cach\right)\)
Chọn 2 điểm trên d1 \(C^2_{17}\left(cach\right)\)
\(\Rightarrow C^1_{20}.C^2_{17}\left(tam-giac\right)\)
\(\Rightarrow C^1_{17}.C^2_{20}+C^2_{17}.C^1_{20}=...\left(tam-giac\right)\)

Đáp án là C
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d 1 và 2 điểm thuộc d 2 : có c 17 1 . c 20 1 tam giác.
TH2. Chọn 2 điểm thuộc d 1 và 1 điểm thuộc d 2 : có c 17 2 . c 20 1 tam giác.
Như vậy, ta có C 17 1 . C 20 1 + C 17 2 . C 20 1 = 5950 tam giác cần tìm.

Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
![]()

Đáp án B
Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
![]()

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
Đáp án C