Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác AIC và BID:
CI = ID ( AB và CD cát hau tại TĐ) (gt)
\(\widehat{I1}=\widehat{I2}\)(đ đ)
AI = IB (gt)
Vậy tam gics AIC = BID (c.g.c)
Vì tam giác AIC =BID nên \(\widehat{C}=\widehat{D}\)(slt)
Vậy BC // AD

Cm tg AOC và Tg BOD(c.g.c)
=>AC=BD
Cm tgCOd và tg DOA(c.g.c)
=>BC=AD
tiếp theo cm ABC = BAD(c.c.c)

5. ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\) \(a.b=c.d\)
\(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2-2ab}{\left(c+d\right)^2-2cd}\)
Mà a+b = c+ d; ab = cd
=> đfcm
Bài 4:
a: Ta có: I nằm trên đường trung trực của AD
nên IA=ID
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔIAB=ΔIDC

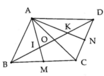
a:Xét ΔAIC và ΔBID có
IA=IB
\(\widehat{AIC}=\widehat{BID}\)
IC=ID
Do đó: ΔAIC=ΔBID
Xét ΔAID và ΔBIC có
IA=IB
\(\widehat{AID}=\widehat{BIC}\)
ID=IC
Do đó: ΔAID=ΔBIC
b: Xét tứ giác ADBC có
I là trung điểm của AB
I là trung điểm của CD
Do đó: ADBC là hình bình hành
Suy ra: AC//BD và AD//BC
c: Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Xét ΔCAD và ΔDBC có
CA=DB
AD=BC
CD chung
Do đó: ΔCAD=ΔDBC