Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+)Đường kính của dây là
d
1
= 0,6mm, suy ra tiết diện dây là: 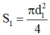
+)Đường kính dây giảm xuống còn
d
2
= 0,4mm, suy ra tiết diện dây là: 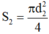
Áp dụng kết quả thu được từ bài 8.11 ta có: 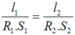
Thay R 1 = R 2 (vì không thay đổi điện trở của dây nung) ta được:
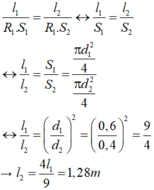

+) Dây thứ nhất có đường kính tiết diện d 1 = 0,5mm, suy ra tiết diện là:
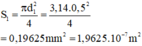
+) Dây thứ hai có đường kính tiết diện d 2 = 0,3mm, suy ra tiết diện là:
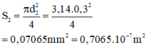
Lập tỉ lệ:
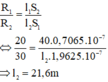

Tóm tắt
\(\rho=0,4.10^{-6}\Omega.m\\ S_1=0,5mm^2=0,5.10^{-6}m^2\\ l_1=4,68m\\ d=0,3mm=3.10^{-4}m\\ l_2=?m\)
Giải
Điện trở của dây thứ nhất là:
\(R=\rho\cdot\dfrac{l_1}{S_1}=0,4.10^{-6}\cdot\dfrac{4,68}{0,5.10^{-6}}=3,744\Omega\)
Chiều dài của dây thứ hai là:
\(R=\rho\cdot\dfrac{l_2}{S_2}\Rightarrow l_2=\dfrac{R.S_2}{\rho}=\dfrac{3,744.3.10^{-4}.3,14}{0,4.10^{-6}}=8817,12m\)

Tiết diện của dây thứ nhất: \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,7.10^{-8}1}{25}=6,8.10^{-10}m^2\)
Vì hai dây này làm cùng một chất liệu nên điện trở suất của chúng là như nhau.
Điện trở của dây thứ hai: \(R=p\dfrac{l}{S}=1,7.10^{-8}\dfrac{0,32}{6,8.10^{-10}}=8\Omega\)

Điện trở: \(R=p\dfrac{l}{S}=5,5.10^{-8}\dfrac{11}{0,55.10^{-6}}=1,1\Omega\)
Điện trở đoạn dây 3m: \(R'=p\dfrac{l'}{S}=5,5.10^{-8}\dfrac{3}{0,55.10^{-6}}=0,3\Omega\)
Điện trở của đoạn dây còn lại: 1\(R''=R-R'=1,1-0.3=0,8\Omega\)
Chiều dài: \(R=p\dfrac{l}{S}\Rightarrow l=\dfrac{R.S}{p}=\dfrac{40.0.55.10^{-6}}{5,5.10^{-8}}=400m\)

Đáp án B
Điện trở tỉ lệ với chiều dài, nên dây 30m có điện trở gấp 3 dây 10m. Vậy R = 3.2 = 6Ω.

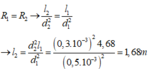
Điện trở dây: \(R=\rho\cdot\dfrac{l}{S}=\rho\cdot\dfrac{l}{\pi\cdot R^2}\)
Như vậy, chiều dài dây và bán kính tiết diện tỉ lệ thuận. Ta có mối quan hệ:
\(\dfrac{l_1}{R_1^2}=\dfrac{l_2}{R_2^2}\Rightarrow\dfrac{l_1}{l_2}=\dfrac{R_1^2}{R_2^2}\Rightarrow\dfrac{3}{l_2}=\dfrac{0,3^2}{0,1^2}\)
\(\Rightarrow l_2=\dfrac{1}{3}m\)