Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

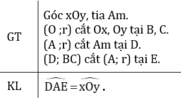
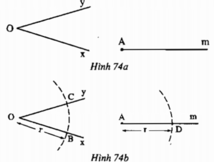
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
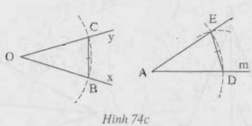
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
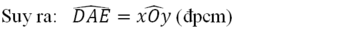

Xét tam giác OBC và tam giác AED có
OB = AE (GT)
OC = AD (GT)
BC = ED (GT)
=> tam giác OBC = tam giác AED
=> góc xOy = góc DAE (2 góc tương ứng)
Vậy góc xOy = góc DAE

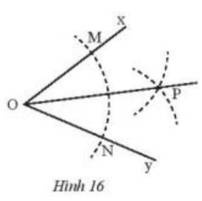
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)