Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
Lời giải:
Theo đề bài ta có:
\(\left\{{}\begin{matrix}\widehat{xOy}=90^o\\d\perp OB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}Ox\perp Oy\\d\perp OB\end{matrix}\right.\)( d là đường trung trực của OB)
Vì theo đề bài,\(B\) nằm trên \(Oy\) nên \(Ox\perp Oy\Leftrightarrow Ox\perp OB\)
Vì thế: \(\left\{{}\begin{matrix}Ox\perp OB\\d\perp OB\end{matrix}\right.\Leftrightarrow Ox//d\left(đpcm\right)\)
Giả sử:
\(d\) không cắt \(AB\)
Vì \(d\) và \(AB\) phân biệt nên \(d//AB\)
Lại có:Theo đề bài thì \(A\) nằm trên \(Ox\),\(B\) nằm trên \(Oy\)(\(\widehat{xOy}\) vuông) nên
\(AB\) không thể song song với \(Ox\)
Khi đó:
\(AB\) không thể song song với \(d\)( vì \(d//Ox\))
Nên điều giả sử sai,\(d\) cắt \(AB\)

bn tự vẽ hình nhé.
vì d là đg trung trực của OA (gt)
=> d vuông góc với OA (hoặc Ox)
ta có: Ox vuông góc với Oy (gt)
Ox vuông góc với d (cmt)
=> Oy // d ( quan hệ từ vuông góc đến song song )
hok tốt

Vì Ad//Oy
=> xOA = dAy = 90° (Vì 2 góc này ở vị trí đồng vị )
=> Ad vuông góc với Oy
Hay đường thẳng d vuông góc với Oy
Vì OA = AB
=> Đường thẳng d là trung trực OB

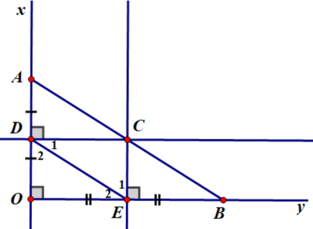
Chứng minh tương tự như d suy ra CB // DE.
Do đó theo tiên đề Ơ-clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.