Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho góc xOy nhọn và điểm A cố định thuộc tia Ox, điểm B di động trên tia Oy. Điểm C là điểm đối xứng của A qua B. Hỏi C di động trên đường nào

Vẽ CQ vuông góc đường thẳng OA tại Q.
mà OB vuông góc OA (vì góc xOy vuông)
\(\Rightarrow OB\) song song CQ
\(\Delta ACQ\)có B là trung điểm AC
OB song song CQ (cmt)
\(\Rightarrow\)O là trung điểm AQ hay Q đối xứng A qua O
* VẬY bất kỳ vị trí của điểm B trên tia Ox thì điểm C luôn di chuyển trên đường thẳng đối xứng với A qua O và vuông góc với OA

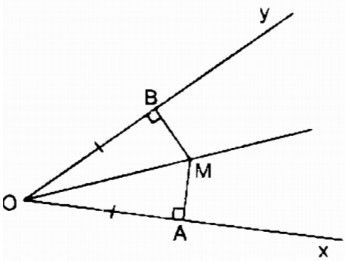
Xét hai tam giác vuông MOA và MOB:
\(\widehat{MAO}=\widehat{MBO}=90^0\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒\(\widehat{AOM}=\widehat{BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat{AOM}=\widehat{BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.

