Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét tam giác AOD VÀ COB có AO=OC ,OB=OD ,chung góc O=> tam giác AOD =tam giác COB(cgc)=>AD=BC
b) Ta có OA=OC,OB=OC=> AB=CD.
Tam giác AOD=tg COB=> góc OAD =góc BCO góc
Và ADO=gócCBO(2 góc tương ứng).
Mà góc ABI + góc CBO=180 độ(kề bù)
góc CDI+góc ADO=180 độ (kề bù)
=> Góc CBO=ADO
Xét tg ABI và tg CDI có AB= CD(cm trên),gics CBO= góc ADO,góc OAC= BCO=> tg ABI=th CDI => AI=CI,BI=Di

HÌnh bạn tự vẽ (vẽ góc nhọn)
a) Xét \(\Delta COB\)và \(\Delta AOD\)ta có:
OB=OA
Góc xOy chung
OC=OD
\(\Rightarrow\Delta COB=\Delta AOD\left(c-g-c\right)\)
\(\Rightarrow BC=AD\)(cặp cạnh tương ứng)
b) Bạn ghi lại, đề bài sai nên phần c chưa làm đc!

Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
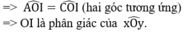

- ΔAOD = ΔCOB
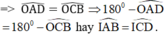
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
- Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
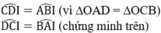
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)

a) Xét 2 tam giác vuông OAC và tam giác OBD có:
OA = OB (gt)
O là góc chung
suy ra tam giác OAC = tam giác OBD (cạnh góc vuông - góc nhọn kề cạnh ấy)
b) Ta có : OD = OA + AD
OC = OB + BC
mà OD = OC (vì tam giác OAC = tam giác OBD)
OA = OB ( gt)
suy ra AD = BC
Xét 2 tam giác vuông ADI và tam giác BCI có:
AD = BC (cmt)
góc D = góc C (vì tam giác OAC = tam giác OBD)
suy ra tam giác ADI và tam giác BCI (cạnh goác vuông - góc nhọn kề cạnh ấy)
suy ra IA = IB (2 cạnh tương ứng)
c)Xét 2 tam giác vuông OAI và tam giác OBI có:
OI là cạnh chung
OA = OB (gt)
suy ra tam giác OAI = tam giác OBI (2 cạnh góc vuông)
suy ra góc O1 = góc O2 (2 góc tương ứng)
suy ra OI là tia phân giác của góc xOy
Cái chỗ A1, A2, B1, B2 bạn đừng kí hiệu vào bài làm nhé!
Mình nhầm tí!

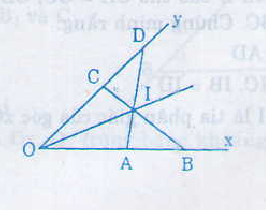
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB =>
=> (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
( ∆AOD = ∆COB)
(chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=>
=> OI là phân giác của
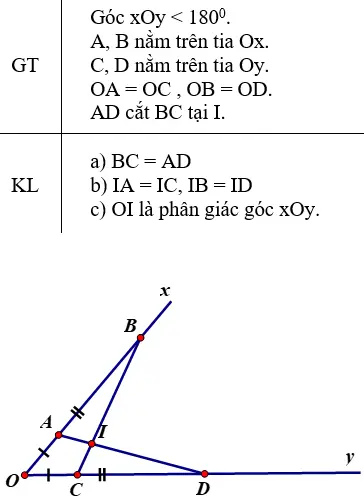
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
b) – ΔAOD = ΔCOB
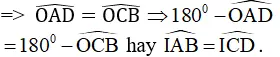
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
– Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
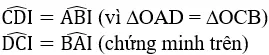
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
c) Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
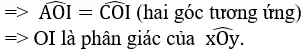

a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC

b) ∆AOD = ∆COB =>
=> (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
( ∆AOD = ∆COB)
(chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=>
=> OI là phân giác của
Hướng dẫn:
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
ˆxOyxOy^ là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC

b) ∆AOD = ∆COB => ˆAOD=ˆOCBAOD^=OCB^
=> ˆBAI=ˆDCIBAI^=DCI^ (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
ˆDCI=ˆABIDCI^=ABI^ ( ∆AOD = ∆COB)
ˆBAI=ˆDCIBAI^=DCI^ (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> ˆCOI=ˆAOICOI^=AOI^
=> OI là phân giác của ˆxOy
