K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

7 tháng 10 2021
Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC

CM
18 tháng 2 2018
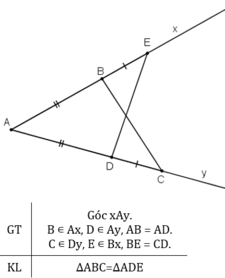
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)
là tam giác có 3 cạnh bằng nhau
chi tiết hơn được không ?