Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOMA vuông tại A và ΔOMB vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOMA=ΔOMB
Suy ra: MA=MB và OA=OB
hay ΔOBA cân tại O
b: Xét ΔOAE vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOE}\) chung
Do đó: ΔOAE=ΔOBD
Suy ra: OD=OE
Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
AD=BE
\(\widehat{MDA}=\widehat{MEB}\)
Do đó: ΔMAD=ΔMBE
Suy ra: MD=ME
c: Ta có: ΔODE cân tại O
mà OM là phân giác
nên OM vuông góc với DE

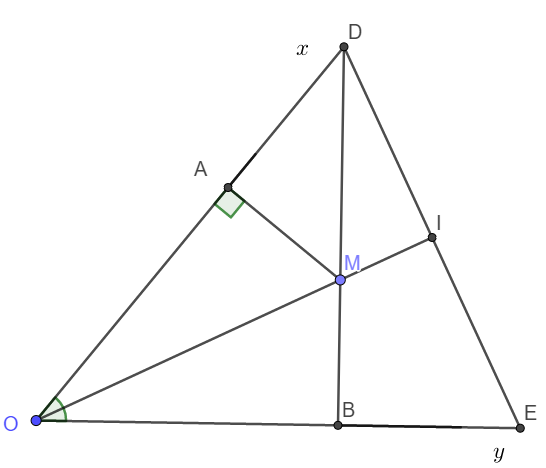
a) Xét tam giác vuông AOM và tam giác vuông BƠM có:
Cạnh huyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) (Cạnh huyền - góc nhọn)
\(\Rightarrow MA=MB;OA=AB\)hay tam giác OAB cân tại O.
b) Xét tam giác vuông AMD và tam giác vuông BME có:
AM = BM
\(\widehat{AMD}=\widehat{BME}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMD=\Delta BME\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow MD=ME\)
c) Ta thấy OA = OB; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\left(c-g-c\right)\)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.

a,b: Xét ΔOAM vuông tại A và ΔOBM vuông tạiB co
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>OA=OB và MA=MB
=>ΔOAB cân tại O
c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
MA=MB
góc AMD=góc BME
=>ΔMAD=ΔMBE
=>MD=ME

a) Xét tam giác vuông MOA và tam giác vuông MOB
có OM là cạnh chung
góc MOA=góc MOB (GT)
suy ra tam giác MOA = tam giác MOB (cạnh huyền-góc nhọn) (1)
suy ra MA=MB
b) từ (1) suy ra OA=OB suy ra tam giác OAB cân tại O (T/chất tam giác cân)
c) Chưa hết đề bài em nhé

Em tham khảo tại link dưới đây nhé.
Câu hỏi của trần thị thúy vân - Toán lớp 7 - Học toán với OnlineMath